Bloch Equations
What are the Bloch equations?
|
|
In 1946 Felix Bloch published a mathematical analysis of the "Nuclear Induction" phenomenon including a set of equations explaining the origin and properties of the NMR signal. This paper is very readable and does not require a high level of mathematics or physics background.
|
Bloch began with the assumption that the millions of individual nuclei in a sample could be represented by a single vector M. (Bloch called M the "polarization" but today it is more frequently known as the net magnetization.) Just as individual nuclei possess spin angular momentum, so does the vector M. As Joseph Larmor showed a half century before, an external field (B) produces a torque (τ) or "twisting force" on M resulting in its precession at angular frequency ω = γ B.
Since M is a vector rotating in space it can be resolved into have three components — Mx(t), My(t), and Mz(t) — each a function of time. Mx(t) and My(t) are the transverse components; Mz(t) is the longitudinal component. |
A torque or twisting force (τ) results from the interaction of net magnetic angular momentum (M) and the magnetic field (M), defined as the vector cross product τ = M x B. The direction of τ is perpendicular to both M and B according to the right-hand rule. This torque causes M to precess around B as shown.
|
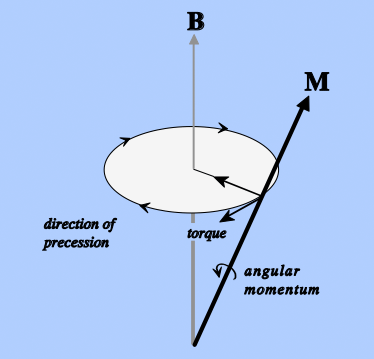
For the case of simple precession of M in a cone around B, the longitudinal component is a constant, Mz(t) = C. The transverse components rotate sinusoidally around the z-direction at angular frequency ω. For simplicity we can adjust their phases so Mx(t) = 0 at t = 0, allowing us to write Mx(t) = A sin ωt and My(t) = A cos ωt, where A is a scaling factor.
Nuclear induction signal recorded by Bloch et al (1946). As the magnetic field was increased (from left to right on the oscilloscope tracing), a transient induction voltage peak was detected in the receiver coil as the system swept through resonance.
|
The "nuclear induction signal" recorded by Bloch et al in their famous experiment reflected the generation of a small current in their receiver coil from the precession of M around B. Like Purcell's group, Bloch et al carried out a continuous wave (CW) NMR experiment where the RF transmit field (B1) was kept constant as the magnetic field was varied and the system swept through resonance.
|
Bloch and colleagues recognized that the NMR nuclear induction signal they had recorded was a transient phenomenon. They even made estimates on how quickly this signal died out as a function of type of material studied (water vs paraffin vs a paramagnetic solution) and the rate of change of the applied magnetic field.
Bloch reasoned that NMR signal decay occurrs because the individual spins that comprise M interact with each other and their environment. As such, M would not precess indefinitely around B, but would instead seek to return to its initial alignment parallel to B with equilibrium magnitude Mo. To do this, the spin system had to release its energy to the environment, a process Bloch termed relaxation.
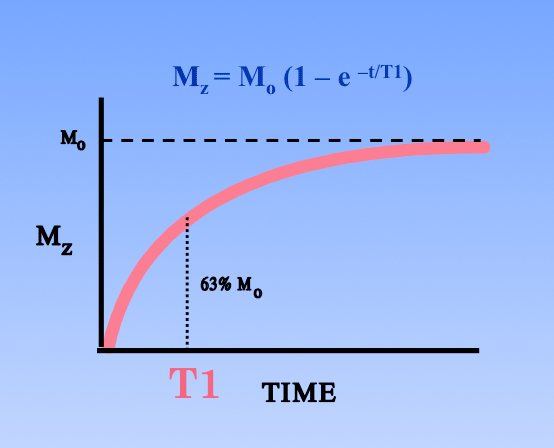
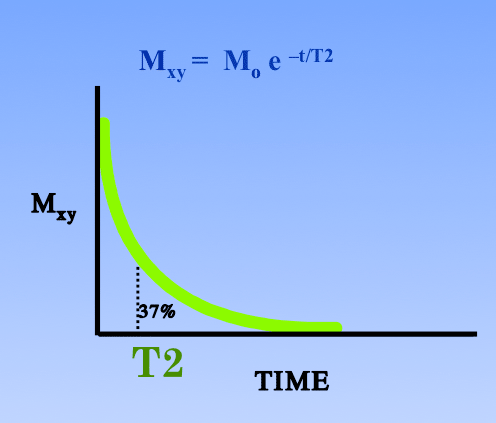
Bloch introduced two relaxation time constants, which he called T1 and T2, to account for the reestablishment of thermal equilibrium of the nuclear magnetization after generation of the NMR signal. T1 reflected the regrowth of longitudinal magnetization (Mz), whereas T2 characterized the decay of the transverse components (Mx and My).
Bloch assumed that T1 and T2 relaxation followed first-order kinetics, such as that seen with the decay of a radioisotope. Furthermore, he assumed that single (rather than multiple) time constants were sufficient to describe this process. T1 and T2 were defined phenomenologically and were not derived from fundamental principles. Although Bloch did not specify the physical mechanisms giving rise to T1 and T2, he did correctly conclude that T1 must result from thermal agitation and T2 from internuclear actions. (The true atomic and molecular origins of T1 and T2 relaxation are considered in much greater detail in multiple subsequent Q&A's).
Bloch reasoned that NMR signal decay occurrs because the individual spins that comprise M interact with each other and their environment. As such, M would not precess indefinitely around B, but would instead seek to return to its initial alignment parallel to B with equilibrium magnitude Mo. To do this, the spin system had to release its energy to the environment, a process Bloch termed relaxation.
Bloch introduced two relaxation time constants, which he called T1 and T2, to account for the reestablishment of thermal equilibrium of the nuclear magnetization after generation of the NMR signal. T1 reflected the regrowth of longitudinal magnetization (Mz), whereas T2 characterized the decay of the transverse components (Mx and My).
Bloch assumed that T1 and T2 relaxation followed first-order kinetics, such as that seen with the decay of a radioisotope. Furthermore, he assumed that single (rather than multiple) time constants were sufficient to describe this process. T1 and T2 were defined phenomenologically and were not derived from fundamental principles. Although Bloch did not specify the physical mechanisms giving rise to T1 and T2, he did correctly conclude that T1 must result from thermal agitation and T2 from internuclear actions. (The true atomic and molecular origins of T1 and T2 relaxation are considered in much greater detail in multiple subsequent Q&A's).
|
Bloch then modified his original vector equation to account for T1 and T2 effects. Specifically, during return to equilibrium, the equations of motion for M in simplified form after a 90°-pulse become
Mx(t) = Mo e −t/T2 sin ωt My(t) = Mo e−t/T2 cos ωt Mz(t) = Mo (1 − e−t/T1) |
|
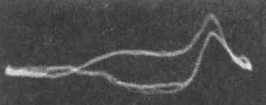
These equations predict that M will exhibit a spiraling precession around B at the Larmor frequency with decay of transverse components back to zero and regrowth of the longitudinal component to its original maximum value Mo. Because T2 is always shorter than T1, the transverse components typically decay completely before the longitudinal magnetization is fully restored. The spiral pattern is sometimes said to resemble a "tent".
The longitudinal relaxation time, T1, therefore represents the time required for Mz to grow from 0 to (1 − 1/e), or about 63% of its final value. Similarly, the transverse relaxation time, T2, represents the time required for Mx or My to decay down to 1/e (about 37%) of their initial maximum values.
Graphical representations of T1 and T2
|
|
References
Bloch F. Nuclear induction. Phys Rev 1946; 70:460-474,1946. (This is the original paper in which Bloch derives his famous equations. Everyone serious about NMR should at least look over this paper — it is very readable, even by those with little math or physics background — many more words and explanations than equations. Besides calling the phenomenon "nuclear induction", the only major difference in terminology is that Bloch used Ho and H1 to refer to the main and radiofrequency magnetic fields, whereas the modern preference is to use Bo and B1.)
Bloch F, Hansen WW, Packard M. The nuclear induction experiment. Phys Rev 1946;70:474-485. (A detailed account of their apparatus and experiment).
Bloch F. Nuclear induction. Phys Rev 1946; 70:460-474,1946. (This is the original paper in which Bloch derives his famous equations. Everyone serious about NMR should at least look over this paper — it is very readable, even by those with little math or physics background — many more words and explanations than equations. Besides calling the phenomenon "nuclear induction", the only major difference in terminology is that Bloch used Ho and H1 to refer to the main and radiofrequency magnetic fields, whereas the modern preference is to use Bo and B1.)
Bloch F, Hansen WW, Packard M. The nuclear induction experiment. Phys Rev 1946;70:474-485. (A detailed account of their apparatus and experiment).
Related Questions
Who discovered NMR?
Who discovered NMR?