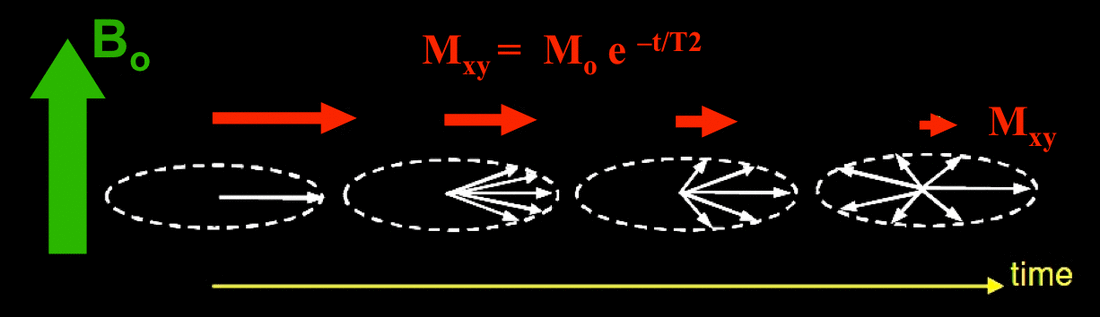
T2 Relaxation: Definition
What is T2 relaxation?
|
|
T2 relaxation is the process by which the transverse components of magnetization (Mxy) decay or dephase. As originally described by Felix Bloch (1946), T2 relaxation is considered to follow first order kinetics, resulting in a simple exponential decay (like a radio-isotope) with time constant T2. Thus T2 is the time required for the transverse magnetization to fall to approximately 37% (1/e) of its initial value. Synonyms for T2 relaxation are transverse relaxation and spin-spin relaxation. (I discourage using the second synonym because "spin-spin" interactions are just one of several mechanisms by which T2 relaxation can occur.)
Diagram showing loss of Mxy component of magnetization and T2. This diagram, like most others, is misleading in that only a tiny fraction of spins ever have transverse phase coherence.
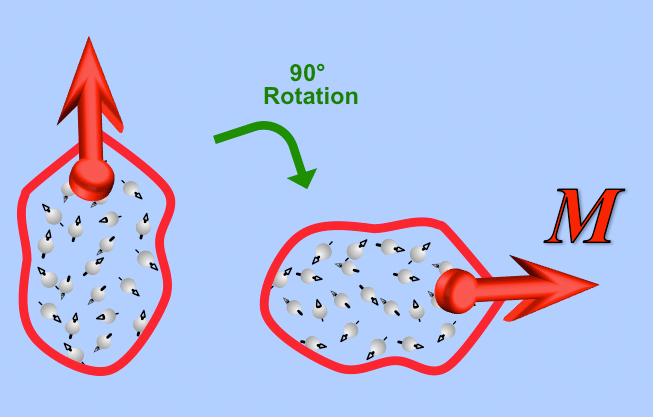
Recall from a previous Q&A that tipping the net magnetization (M) into the transverse plane does not cause all the spins to magically lock in phase. What happens is that those same spins initially showing some statistical "preference" for the z-direction prior to the RF-pulse have now been rotated into the transverse plane. The initial Boltzmann distribution "ordering" of spins in the z-direction has been has been preserved and transformed by the rotation into what can be considered "phase coherence" in the xy-plane. Simultaneously, the initial value of M in the z-direction (Mz) immediately before the RF-pulse has been converted to a net transverse magnetization (Mxy) after the pulse. The diagrams below, although still not perfect, are perhaps a little closer to what really happens.
The spin system begins with an slightly unequal distribution of angular momentum in the z-direction, creating a net magnetization (M). The 90°-pulse rotates the entire system converting the initial asymmetry of z-components into asymmetry of transverse (xy)-components resulting in a temporary statistical "phase coherence".
|
After the 90°-pulse there is an asymmetric statistical clustering of spins in the transverse plane which constitutes "phase coherence". Only a tiny fraction (~10-6) of spins contribute to this phenomenon. The number of these spins has been grossly and disproportionately exaggerated in the diagram.
|
Now tipped into the xy-plane and the RF-pulse over, the transverse spin components (represented by small black arrows in the drawing above) and their vector sum (Mxy) will precess within the plane at the Larmor frequency. It is the sweep of this transverse magnetization (Mxy) that induces a current in the receiver coils and is solely responsible for generating the MR signal.
The presence of a non-zero net transverse magnetization (Mxy) is at any time is evidence of persistent asymmetry of transverse components of angular momentum, and what is commonly called "phase coherence." Any process that disrupts either the number or relative positions of these transverse components will result in T2 relaxation. These fall into one of two general categories:
The presence of a non-zero net transverse magnetization (Mxy) is at any time is evidence of persistent asymmetry of transverse components of angular momentum, and what is commonly called "phase coherence." Any process that disrupts either the number or relative positions of these transverse components will result in T2 relaxation. These fall into one of two general categories:
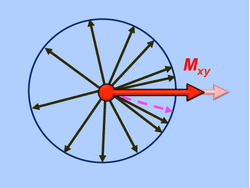
Loss of spin from T1 interaction
T2 Relaxation Accompanying T1 Relaxation
As described in the prior Q&A, T1 relaxation occurs when a spin exchanges energy with its external environment. If such an energy exchange were to affect one of the spins contributing to Mxy, both the transverse and longitudinal components of its angular momentum would be randomly changed and it would immediately lose phase relations with other spins. You can think of its arrow as simply "dropping out" of the diagram. Without that spin's small contribution, the value of Mxy would be diminished and so T2 relaxation would have occurred. Thus, any process causing T1 relaxation also results in T2 relaxation. This is sometimes called the "T1 contribution to T2" or "T1 in T2".
As described in the prior Q&A, T1 relaxation occurs when a spin exchanges energy with its external environment. If such an energy exchange were to affect one of the spins contributing to Mxy, both the transverse and longitudinal components of its angular momentum would be randomly changed and it would immediately lose phase relations with other spins. You can think of its arrow as simply "dropping out" of the diagram. Without that spin's small contribution, the value of Mxy would be diminished and so T2 relaxation would have occurred. Thus, any process causing T1 relaxation also results in T2 relaxation. This is sometimes called the "T1 contribution to T2" or "T1 in T2".
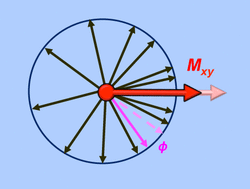
Phase change (ϕ) of a spin due to a local field
T2 Relaxation Occurring Without T1 Relaxation
Although T2 relaxation always accompanies T1 relaxation, T2 relaxation may also occur without T1 relaxation. This is sometimes referred to as the "secular contribution to T2."
One of the most common ways for this to occur is for a spin to be located in a molecular environment where it experiences a local static field disturbance (Bloc) in addition to the main magnetic field (Bo). For example, the spin might be located on a water molecule diffusing by an iron-containing clump of hemosiderin or reside on a molecule next to an electronegative oxygen atom.
If Bloc is in the same (z-) direction as Bo, the two static fields add together and a spin within that
altered local environment would now precess at frequency γ(Bo + Bloc). Meanwhile, the other unaffected spins would still be precessing at the original Larmor frequency (fo = γBo). Over time (t) a phase difference of ϕ = γBloc•t would develop between the spin and its colleagues. With this spin now out of step with the others, the net transverse magnetization (Mxy) would be diminished. In other words, T2 relaxation would have occurred.
Although T2 relaxation always accompanies T1 relaxation, T2 relaxation may also occur without T1 relaxation. This is sometimes referred to as the "secular contribution to T2."
One of the most common ways for this to occur is for a spin to be located in a molecular environment where it experiences a local static field disturbance (Bloc) in addition to the main magnetic field (Bo). For example, the spin might be located on a water molecule diffusing by an iron-containing clump of hemosiderin or reside on a molecule next to an electronegative oxygen atom.
If Bloc is in the same (z-) direction as Bo, the two static fields add together and a spin within that
altered local environment would now precess at frequency γ(Bo + Bloc). Meanwhile, the other unaffected spins would still be precessing at the original Larmor frequency (fo = γBo). Over time (t) a phase difference of ϕ = γBloc•t would develop between the spin and its colleagues. With this spin now out of step with the others, the net transverse magnetization (Mxy) would be diminished. In other words, T2 relaxation would have occurred.
|
T2 relaxation without T1 relaxation can also happen in a special form of dipolar interaction known informally as a spin-spin "flip-flop". In this mechanism a pair of spins simultaneously exchange their longitudinal angular momentum components resulting in no net T1 effect but loss of T2 coherence.
|
Spin-spin "flip-flop". A pair of spins exchanges longitudinal angular momentum going from state {up|down} to state {down|up}. There is no change in T1 but the interaction produces T2 relaxation.
|
The basic concepts of T2 relaxation are summarized below.
T2 Relaxation Summary |
References
Bloch F. Nuclear induction. Phys Rev 1946; 70:460-474,1946. (This is the original paper in which Bloch derives his famous equations and defines T1 and T2. Everyone serious about NMR should at least look over this paper -- it is very readable, even by those with little math or physics background -- many more words and explanations than equations.)
Bloch F. Nuclear induction. Phys Rev 1946; 70:460-474,1946. (This is the original paper in which Bloch derives his famous equations and defines T1 and T2. Everyone serious about NMR should at least look over this paper -- it is very readable, even by those with little math or physics background -- many more words and explanations than equations.)