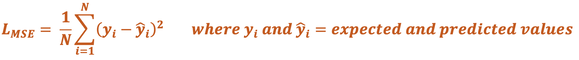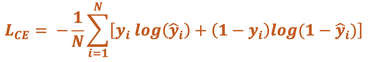In the prior Q&A we briefly described several machine learning techniques (including logistic regression, cluster analysis, and support vector machines) used to classify and subdivide large data sets. Here we explain several important methods to prepare raw data for analysis and to optimally fit it to a given model.
Selecting a Model
In many quantitative data processing scenarios a straightforward model may be relatively easy to select. As a simple example, one may wish to find a relationship between liver and spleen volumes on MRI. Or another — to classify whether a patient has Alzheimer disease, Parkinson disease, or some other dementia based upon the thickness of cortical gray matter. These types of problems could be amenable to modeling by regression or one of the other shallow learning techniques (support vector machine, cluster analysis, random forest) as described in a prior Q&A.
In other situations, such as reducing motion artifacts in an MR image, the best model may not at all be obvious and a generalized deep learning approach (such as a convolutional neural network) is needed. Here the network may be allowed to find its own optimal solution by analyzing in training data that has been partially or fully labeled.
In other situations, such as reducing motion artifacts in an MR image, the best model may not at all be obvious and a generalized deep learning approach (such as a convolutional neural network) is needed. Here the network may be allowed to find its own optimal solution by analyzing in training data that has been partially or fully labeled.
Data Preparation
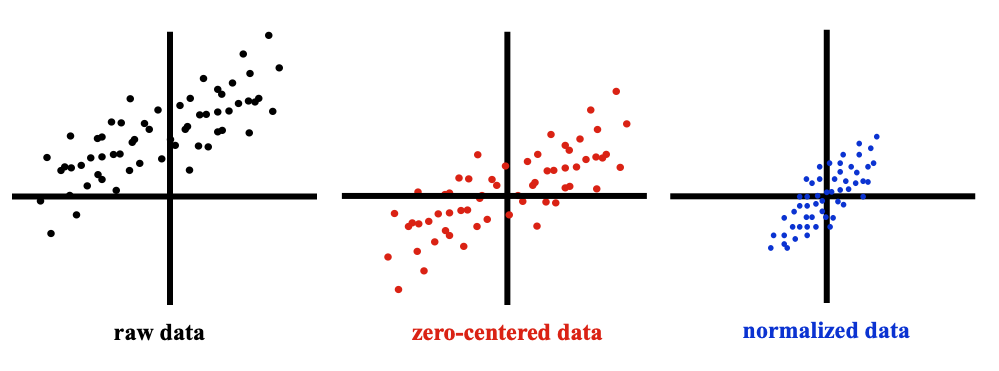
The first recommended step is to normalize the data. This is typically done by zero-centering it in each direction, then normalizing it to have a mean of 0 and standard deviation of 1 along each direction.
Initializing Model Parameters
Prior to training the network, initialization of network parameters such as weights and biases for each neuron must be selected. One popular choice (a version of the Xavier initialization) is to set starting parameters with values drawn randomly from a Gaussian distribution of mean = 0 and standard deviation = √(2/n), where n = the number of inputs + outputs for each neuron. A even better method may be the He initialization (optimized for ReLU activations), where n = the number of inputs only.
In truth, AI application developers seldom start with such highly randomized initialization parameters. Instead, they often employ a transfer learning approach, copying weights and biases from other tested networks as a starting point. This approach can significantly reduce training time for the new network being designed.
Training
After selecting a model and preparing the raw data, training of the network must take place. For image-based applications, a supervised learning technique is most commonly used. The data scientists will likely have at their disposal a reasonably large number of cases (usually in the thousands or higher) that contain images each with an independently verified label serving as "ground truth". For example, the cases might all be MR images of brain tumors together with a binary label (e.g., benign or malignant).
Armed with this labeled data set, the investigators will save out a relatively small proportion (10-15%) of the whole to be used as a validation set after the network has been fully trained. The other labeled samples (85-90%) will form the training set. For computational efficiency, this training data is usually divided into batches (typically of size 32, 64, 128, or another factor of 2). After each training batch is passed through the network, the predicted output from the network is compared to the table of ground truths and a loss function (error score) is calculated. Weighting factors and parameters of the network are then modified in an iterative fashion to minimize the loss function. Usually iterations of several batches are needed so that all training examples have had a chance to have been fed through the network. At this point an epoch is said to have been completed. To fully train the network many epochs are needed, often in the hundreds or thousands, which can take hours or days even on fast computers.
The Loss Function
The Loss Function, also sometimes known as the Cost or Error Function, is a measure of the level of error in a network's output when using a certain set of internal parameters (such as weights and biases). Two loss functions are commonly used:
Mean Squared Error (MSE) Loss. This is average of the squared differences between the expected and predicted values, given by the formula
MSE Loss functions are typically used when the outcome is numeric, such as a distance measurement or volume. This is the metric by which linear regression is optimized.
Cross-Entropy (CE) Loss. Also known as Logistic Loss or Log Loss, this method penalizes errors using a non-linear function (logarithm). When the difference between expected and predicted values is small, the penalty is small; but when the difference is large, the penalty can be enormous. The CE Loss formula for a binary classification system is written as
Cross-Entropy (CE) Loss. Also known as Logistic Loss or Log Loss, this method penalizes errors using a non-linear function (logarithm). When the difference between expected and predicted values is small, the penalty is small; but when the difference is large, the penalty can be enormous. The CE Loss formula for a binary classification system is written as
Overfitting and Underfitting
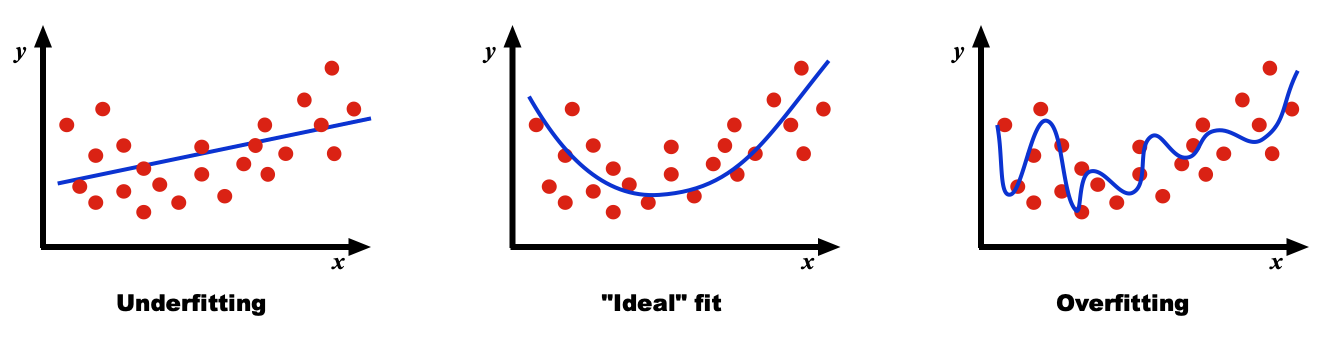
What is the optimal number of parameters to optimally fit a set of data? As all data sets vary, there is no general answer to this question, but the problems with overfitting and underfitting can be appreciated in the diagrams below:
In underfitting, the model has an insufficient number of parameters to fully learn the data. In overfitting the model is too complex and contains too many parameters. The computational burden is excessive and even though it fits the sample data with high precision, the model is highly optimized for the particular training data and will not generalize well to other data sets.
Regularization
One possible solution to overfitting would be to collect more training data points. However, this is time-consuming and may not be practical if training data is hard to generate. Another option would be to reduce the number of model parameters, but this is a blunt instrument and it is often not clear at the onset how many variables will actually need to be used.
Rather than directly manipulating the number of parameters, a more robust method is to restrict the values that the parameters can take, a process known as regularization. The most commonly used technique is known as L2 regularization, which adds an additional term to the loss function of the form λ(Σw²) where λ is a user-defined constant known as the regularization strength and Σw² is the sum of squared values of the calculated weights at each step of training.
A second and very useful regularization method applicable to most multilayer networks is known as dropout. As the name implies, various nodes and their outputs are randomly ignored or temporarily dropped out of the model during training. Typical dropout rates are about 20% of input nodes and 20-50% of intermediate nodes. (Output nodes do not participate).
Dropout has several direct and indirect effects on the network: 1) it means that the structure of the network will randomly change from time to time, forcing nodes to be more independent; 2) it introduces noise, making the weight calculations less dependent on a particular configuration of training data, thus reducing overfitting; and 3) it may break apart co-dependent nodes that adapt to fix mistakes committed by other nodes in prior layers, thus making the model more robust.
Batch Normalization
Batch normalization is a procedure applied to rescale outputs of intermediate layer neurons during the course of training so that their values are Gaussian with a mean of 0 and standard deviation of 1. Recall that one of the first steps in data preparation was to normalize the input data to the network so that each first layer neuron could expect to receive a consistent range of information. But deeper layers in the network have no such guarantee what their inputs may be (sometimes extremely large or extremely small). They become highly dependent on earlier nodes. By renormalizing inputs to nodes at intermediate layers, training speeds can be markedly improved. Because it restricts large swings in intermediate data, batch normalization is also provides a modest degree of regularization.
Advanced Discussion (show/hide)»
No supplementary material yet. Check back soon!
References
He K, Zhang X, Res S, Sun J. Delving deep into rectifiers: surpassing human-level performance on ImageNet classification. arXiv:1502.01852v1 (6 Feb 2015) - describes an initialization technique optimized for networks with ReLU activations.
Ioffe S, Szegedy C. Batch normalization: accelerating deep network training by reducing internal covariate shift. arXiv:1502.03167v3 (2 Mar 2015)
Karpathy A. CS231n Convolutional Neural Networks for Visual Recognition. Linear Classifiers: Support Vector Machine, Softmax. Stanford University, 2016. [LINK]
Karpathy A. CS231n Convolutional Neural Networks for Visual Recognition. Neural Networks Part 1: Setting up the Architecture. Stanford University, 2016. [LINK]
Karpathy A. CS231n Convolutional Neural Networks for Visual Recognition. Neural Networks Part 2: Setting up the Data and the Loss. Stanford University, 2016. [LINK]
Srivastava N, Hinton GE, Krizhevsky A, et al. Dropout: a simple way to prevent neural networks from overfitting. Journal of Machine Learning Research 2014; 15:1929–1958.
He K, Zhang X, Res S, Sun J. Delving deep into rectifiers: surpassing human-level performance on ImageNet classification. arXiv:1502.01852v1 (6 Feb 2015) - describes an initialization technique optimized for networks with ReLU activations.
Ioffe S, Szegedy C. Batch normalization: accelerating deep network training by reducing internal covariate shift. arXiv:1502.03167v3 (2 Mar 2015)
Karpathy A. CS231n Convolutional Neural Networks for Visual Recognition. Linear Classifiers: Support Vector Machine, Softmax. Stanford University, 2016. [LINK]
Karpathy A. CS231n Convolutional Neural Networks for Visual Recognition. Neural Networks Part 1: Setting up the Architecture. Stanford University, 2016. [LINK]
Karpathy A. CS231n Convolutional Neural Networks for Visual Recognition. Neural Networks Part 2: Setting up the Data and the Loss. Stanford University, 2016. [LINK]
Srivastava N, Hinton GE, Krizhevsky A, et al. Dropout: a simple way to prevent neural networks from overfitting. Journal of Machine Learning Research 2014; 15:1929–1958.
Related Questions
What are the various types of deep networks and how are they used?
What are the various types of deep networks and how are they used?