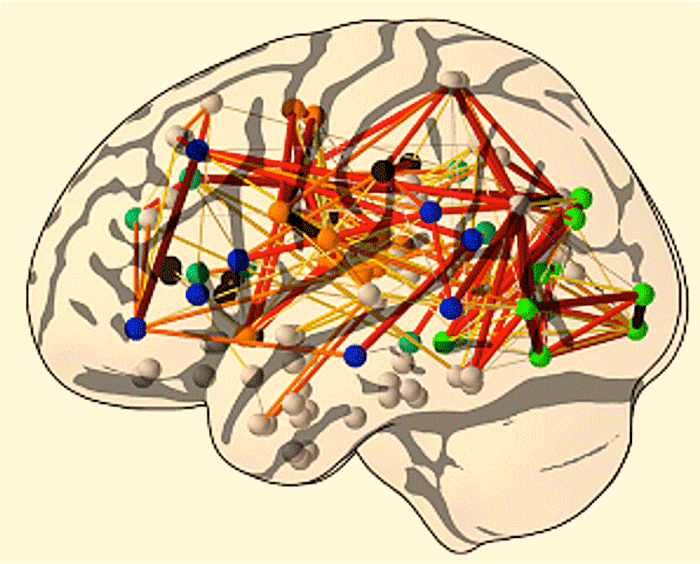
Network/graph theory — used to analyze such diverse systems as telecommunications, computer circuitry, social organizations, and the internet — has become an increasingly popular method for describing functional and anatomic connectivity in the brain. Although one step removed from classic MR physics, network/graph analysis seems poised to become a pre-eminent method for fMRI analysis, so a brief introduction to some of its concepts may be useful.
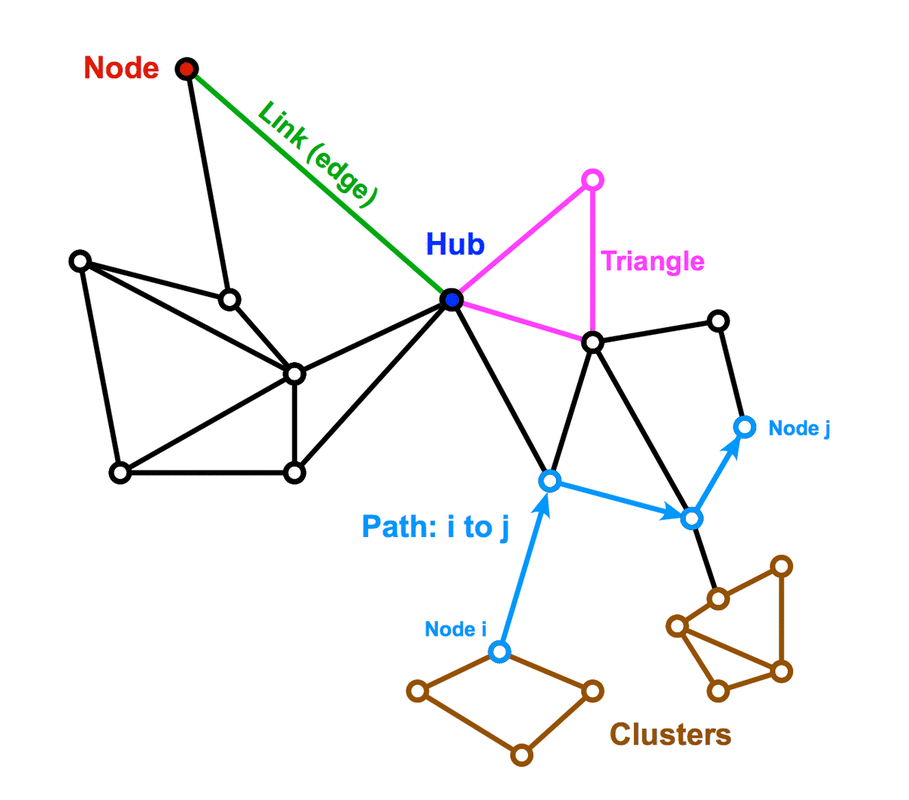
The initial step in network analysis is to define nodes (or vertices): identifiable brain regions thought to function homogeneously in a given experiment. Nodes may be as small as individual voxels, but are more typically somewhat larger anatomic units (such as gyri, nuclei, or areas with a common cytoarchitecture). A link (or edge) joins two nodes that have correlated activity (by fMRI, EEG, MEG, etc.) or a direct physical connection (e.g., from neuroanatomy or diffusion tensor tractography). A network with nodes and links may be represented either graphically or as a numerical array. The latter is known as an adjacency matrix, where each element (eij) is a number reflecting the strength of the link between nodes i and j.
A path is an ordered sequence of links connecting two nodes, whose length is defined as the number of links. Some paris of nodes may be connected by several paths with different lengths. The average length of the shortest paths for all node pairs in a network is called the characteristic path length, a metric inversely related to communication efficiency. Connection density is the ratio of actual number of links to the total number of possible links and is often used as an estimator for energy expenditure, resource utilization, or other physical "cost" of the network.
In a complex system like the brain some nodes will be extensively interconnected while others may remain relatively isolated. The number of connections a node has with the rest of the network is called its degree. A node with a large number of connections is called a hub and said to have a high centrality. Such nodes are often essential to efficient communication in the network.
A cluster refers to a small group of connected nearest neighbor nodes. The smallest cluster is a triangle (3 nodes). Many networks contain smaller subnetworks known as modules. which may be organized hierarchially. The clustering coefficient relates the number of clusters to the size of the entire network. Efficient and complex networks typically have a high degree of clustering.
Many brain networks also demonstrate 'small-world' organization. The small-world concept takes origin from social networks and the phenomenon that even strangers on far sides of the earth can be connected by a relatively small number of mutual acquaintances.
Small world networks are characterized by many hubs, high degrees of local clustering, and short path lengths globally linking all the network nodes. Thus, even though most nodes maintain only a limited number of direct connections in cliques, all nodes of the system can be accessed through a relatively small number of intermediate steps.
Small world networks are characterized by many hubs, high degrees of local clustering, and short path lengths globally linking all the network nodes. Thus, even though most nodes maintain only a limited number of direct connections in cliques, all nodes of the system can be accessed through a relatively small number of intermediate steps.
At present it is not certain which of the many possible network descriptors and metrics listed above will prove most useful, but preliminary studies in disorders such as Alzheimer disease, autism spectrum, and schizophrenia have already identified changes in brain organization identifiable through network measures.
Advanced Discussion (show/hide)»
No supplementary material yet. Check back soon!
References
Bullmore E, Sporns O. Complex brain networks: graph theoretical analysis of structural and functional systems. Nat Rev Neurosci 2009;10:186–98.
Brain Connectivity Toolbox, available at brain-connectivity-toolbox.net. (Best web site for MATLAB-based processing modules and explanation of terms). Contains the following very useful table defining network metrics mathematically (assessed Oct 2016).
De Martino F, Valente G, Staeren N, et al. Combining multivariate voxel selection and
support vector machines for mapping and classification of fMRI spatial patterns. NeuroImage 2008; 43:44–58.
Milgram S. The small-world problem. Psychology Today 1967; 1:61-67. (First elucidation of this concept applied to social networks. Some of Milgram's experimental findings have been criticized, but he may be right after all. The concept is more commonly known as "Six degrees of separation", stating that we are all just six links away from everyone else in the world. This phrase was first coined by Hungarian author Frigyes Karinthy in his 1929 short story, Chains, and later popularized in the eponymous 1990 play of John Guare and its 1993 movie adaptation.)
Pereira F, Mitchell T, Botvinick M. Machine learning classifiers and fMRI: a tutorial overview. NeuroImage 2009; 45:S199–209.
Smith SM, Miller KL, Salimi-Khorshidi G, et al. Network modelling methods for FMRI. NeuroImage 2011; 54:875–891.
Smith SM. The future of FMRI connectivity. NeuroImage 2012;62(2):1257–1266.
Sporns O, Honey CJ, Kotter R. Identification and classification of hubs in brain networks. PLoS One 2007; 2:e1049.
van den Heuvel MP, Hulshoff-Pol HE. Exploring the brain network: a review on resting-state fMRI functional connectivity. Eur Neuropsychopharmacol 2010; 20:519–534.
Watts DJ, Strogatz SH. Collective dynamics of "small-world" networks. Nature 1998; 393:440-442. (Seminal paper on small-world theory and applications)
Bullmore E, Sporns O. Complex brain networks: graph theoretical analysis of structural and functional systems. Nat Rev Neurosci 2009;10:186–98.
Brain Connectivity Toolbox, available at brain-connectivity-toolbox.net. (Best web site for MATLAB-based processing modules and explanation of terms). Contains the following very useful table defining network metrics mathematically (assessed Oct 2016).
De Martino F, Valente G, Staeren N, et al. Combining multivariate voxel selection and
support vector machines for mapping and classification of fMRI spatial patterns. NeuroImage 2008; 43:44–58.
Milgram S. The small-world problem. Psychology Today 1967; 1:61-67. (First elucidation of this concept applied to social networks. Some of Milgram's experimental findings have been criticized, but he may be right after all. The concept is more commonly known as "Six degrees of separation", stating that we are all just six links away from everyone else in the world. This phrase was first coined by Hungarian author Frigyes Karinthy in his 1929 short story, Chains, and later popularized in the eponymous 1990 play of John Guare and its 1993 movie adaptation.)
Pereira F, Mitchell T, Botvinick M. Machine learning classifiers and fMRI: a tutorial overview. NeuroImage 2009; 45:S199–209.
Smith SM, Miller KL, Salimi-Khorshidi G, et al. Network modelling methods for FMRI. NeuroImage 2011; 54:875–891.
Smith SM. The future of FMRI connectivity. NeuroImage 2012;62(2):1257–1266.
Sporns O, Honey CJ, Kotter R. Identification and classification of hubs in brain networks. PLoS One 2007; 2:e1049.
van den Heuvel MP, Hulshoff-Pol HE. Exploring the brain network: a review on resting-state fMRI functional connectivity. Eur Neuropsychopharmacol 2010; 20:519–534.
Watts DJ, Strogatz SH. Collective dynamics of "small-world" networks. Nature 1998; 393:440-442. (Seminal paper on small-world theory and applications)
Related Questions
How do you statistically analyze fMRI data?
How do you process and analyze resting state fMRI data?
Can fMRI read your mind?
How do you statistically analyze fMRI data?
How do you process and analyze resting state fMRI data?
Can fMRI read your mind?