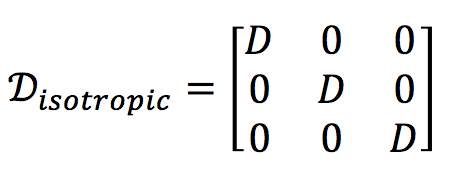Isotropic vs Anisotropic
What is the difference between isotropic and anisotropic diffusion?
|
|
|
For most fluids and some homogeneous solid materials like gels, diffusion is the same in every direction. These substances are called isotropic and are characterized by a single diffusion coefficient (D). Biological tissues, on the other hand, are highly structured and typically have different diffusion coefficients along different directions and are called anisotropic. Virtually all biological materials demonstrate some degree of anisotropy. White matter is highly ansiotropic because of the parallel orientation of its nerve fiber tracts. Other tissues demonstrating significant anisotropy include skeletal muscle and tendons.
|
Dissected brain showing white matter tracts
|
In anisotropic materials, diffusion cannot be described by a single number, but a [3 x 3] array called the diffusion tensor. The three diagonal elements (Dxx, Dyy, Dzz) of the tensor represent diffusion coefficients measured in the laboratory frame of reference along each of the principal (x-, y- and z-) directions. The six off-diagonal terms (Dxy, Dyz, etc) reflect correlation between random motions corresponding to each pair of principal directions.
|
For the special case of perfect isotropic diffusion (such as seen in pure liquids), the off-diagonal elements are all zero. The diagonal elements are all the same and equal the single diffusion coefficient, D, for the isotropic material (i.e., Dxx = Dyy = Dzz = D).
|
The concepts of diffusion anisotropy and the diffusion tensor underlie many advanced processing techniques including DT imaging, fractional anisotropy imaging, and MR tractography. These topics will be addressed in later Q&A's.
References
Beaulieu C. The basis of anisotropic water diffusion in the nervous system - a technical review. NMR Biomed 2002:15:325-455
Kingsley PB. Introduction to diffusion tensor imaging mathematics: Part I. Tensors, rotations and eigenvectors. Concepts Magn Reson Part A 2006; 28A:101-122.
Minati L, Weglarz WP. Physical foundations, models, and methods of diffusion magnetic resonance imaging of the brain: a review. Concepts Magn Reson Part A 2007; 30A:278-307.
Mukherjee P, Berman JI, Chung SW, et al. Diffusion tensor MR imaging and fiber tractography: theoretic underpinnings. AJNR Am J Neuroradiol 2008; 29:632-640.
Beaulieu C. The basis of anisotropic water diffusion in the nervous system - a technical review. NMR Biomed 2002:15:325-455
Kingsley PB. Introduction to diffusion tensor imaging mathematics: Part I. Tensors, rotations and eigenvectors. Concepts Magn Reson Part A 2006; 28A:101-122.
Minati L, Weglarz WP. Physical foundations, models, and methods of diffusion magnetic resonance imaging of the brain: a review. Concepts Magn Reson Part A 2007; 30A:278-307.
Mukherjee P, Berman JI, Chung SW, et al. Diffusion tensor MR imaging and fiber tractography: theoretic underpinnings. AJNR Am J Neuroradiol 2008; 29:632-640.
Related Questions
What is diffusion tensor imaging (DTI) and how does this differ from "regular" diffusion weighted imaging (DWI)?
What is fractional anisotropy (FA)?
What is diffusion tensor imaging (DTI) and how does this differ from "regular" diffusion weighted imaging (DWI)?
What is fractional anisotropy (FA)?