Ernst Angle
How do you pick the "optimum" flip angle?
|
|
The choice of flip angle is critical for determining both signal intensity as well as image contrast. It also depends on the particular pulse sequence utilized. For the purposes of this question we will restate it slightly: Which flip angle gives the maximum signal for a given tissue?
We will further restrict our answer to a particular class of commonly used GRE sequences where transverse coherences (discussed in a later Q&A) are purposely disrupted. These are known as "Spoiled-GRE" sequences and include many with familiar names (FLASH, SPGR, VIBE, T1-FFE, MPGR, MP-RAGE). For now don't worry what spoiling means, as we will cover that in another Q&A very shortly.
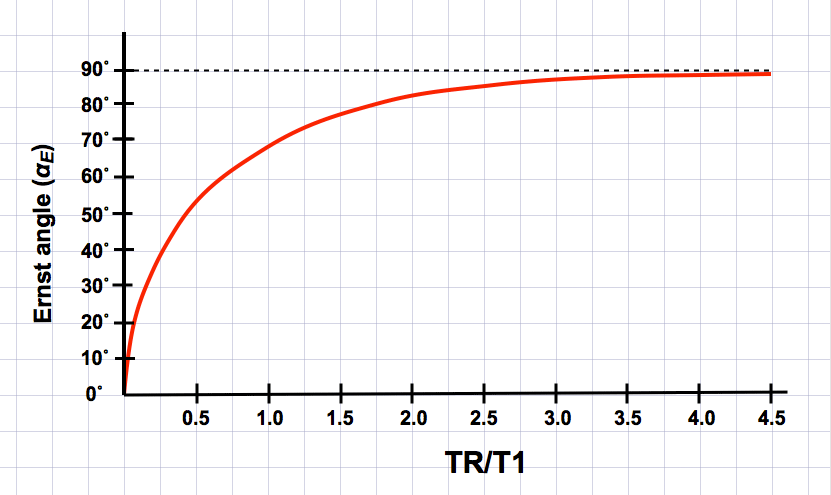
The important result is that for such sequences in which no transverse coherences exist, MR signal is maximized at the Ernst angle (αE), which can be calculated from the equation
We will further restrict our answer to a particular class of commonly used GRE sequences where transverse coherences (discussed in a later Q&A) are purposely disrupted. These are known as "Spoiled-GRE" sequences and include many with familiar names (FLASH, SPGR, VIBE, T1-FFE, MPGR, MP-RAGE). For now don't worry what spoiling means, as we will cover that in another Q&A very shortly.
The important result is that for such sequences in which no transverse coherences exist, MR signal is maximized at the Ernst angle (αE), which can be calculated from the equation
αE = arccos (e−TR/T1)
Note that this equation predicts that the optimal flip angle will be 90° only when TR>>T1.
|
As an example, let us calculate the optimal flip angle for such a sequence in the brain (where the average T1 = 800 msec). When TR = 3000, the Ernst angle is computed to be 89°. In this situation, a conventional 90° pulse is nearly optimal. When TR = 100 msec, however, a different result is obtained. Here the optimal angle is calculated to be only 28°.
|
|
|
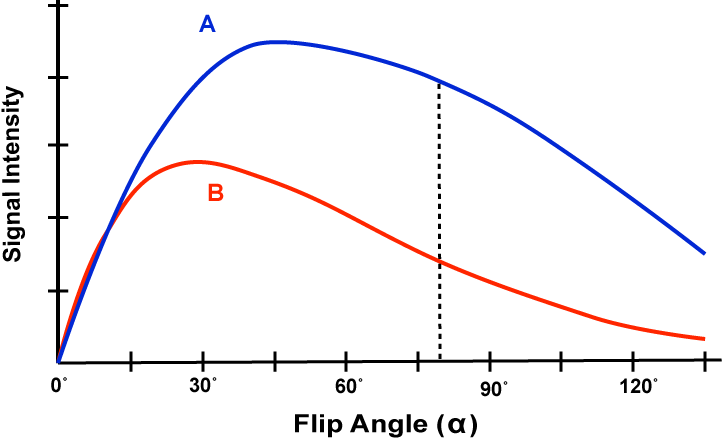
Although the Ernst angle may provide maximum signal intensity on a spoiled-GRE sequence for a single tissue, it does not necessarily maximize the contrast between two different tissues. In the graph left it can be seen that the maximum contrast between tissues A and B is obtained at a flip angle far away from the Ernst angle for either individual tissue.
|
References
Ernst RR, Anderson WA. Application of Fourier transform spectroscopy to magnetic resonance. Rev Sci Instrum 1966; 37:93-102. (Fairly heavy math, but a classic)
Ernst RR, Anderson WA. Application of Fourier transform spectroscopy to magnetic resonance. Rev Sci Instrum 1966; 37:93-102. (Fairly heavy math, but a classic)
Related Questions
What is a partial flip angle pulse, and why would you want to use one?
Wait a minute! If a partial flip angle pulse tips less magnetization into the transverse plane than a 90° pulse does, how can the signal be higher?
What is a partial flip angle pulse, and why would you want to use one?
Wait a minute! If a partial flip angle pulse tips less magnetization into the transverse plane than a 90° pulse does, how can the signal be higher?