Effect of B1 on M

How does B1 tip the net magnetization (M)?  

Before diving into the details of how RF stimulation affects M, let us quickly review what M is and where the B1 field comes from.

Net magnetization (M), the averaged sum of many individual quantum spins, can be treated as a regular vector in classical physics.

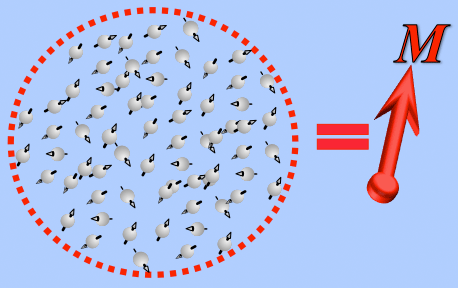
For the purposes of the next several Q&A's, it is probably better to forget completely about individual nuclear spins and consider only the net magnetization (M), the sum of many spins averaged together.  The bizarre aspects of quantum mechanics can then be disregarded and the motion of M analyzed using classical physics.  Think of M as a big spinning bar magnet, if you must.

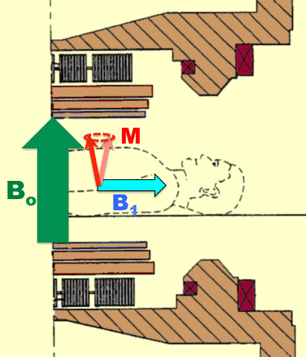
The radiofrequency field (B1) is applied perpendicular to the main magnetic field (Bo). The B1 field is produced either by a local coil (as shown in the picture) or more commonly, from windings in the walls of the scanner itself. Initially, M is aligned with Bo but will be tipped out of alignment during application by the rotating/oscillating B1 field.  Like pushing a child on a swing, the B1 field must be applied near the Larmor frequency for this to occur.

With continued application of the B1 field, M precesses at continually larger angles away from Bo.

Vertical bore scanner showing main (Bo) and RF (B1) fields. M is initially aligned with Bo but will be tipped away by the action of B1, precessing at the resonance frequency.

Continued application of the B1 field results in progressive tipping of the net magnetization away from its initial alignment with Bo. M can be rotated 10°, 90°, 180°, 270°, 836°, or any amount. After every 360° rotation M returns to its initial alignment with Bo.  Some progressive arbitrary rotations of M are shown below.

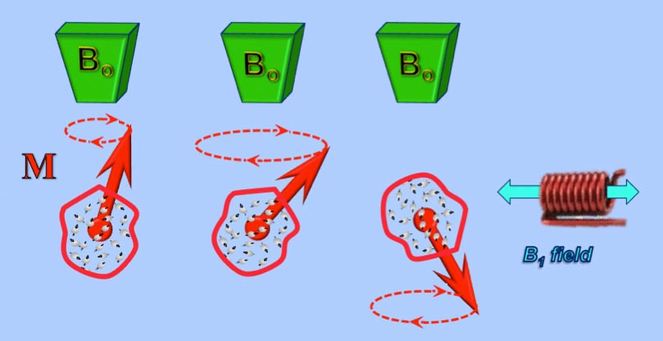
The ambitious diagram below tries to represent what is happening to individual spins at the quantum level as well. Remember that in addition to M, each proton is also precessing around the Bo field individually.  From the Heisenberg uncertainty principle we cannot know the exact direction any particular proton magnetic moment is pointing at any given time.  However, it can be shown that a homogenous B1 field does not change the relative orientation of individual spins. The entire ensemble, like M, is merely rotated by the RF field.  This is why the magnitude of the net magnetization (M) after an RF-pulse is the same as before an RF-pulse, although it is changed in direction.

As long as the B1 field is left on, M can be rotated to any angle. However, neither the magnitude of M nor the relative orientation of spins changes during this rotation.

Advanced Discussion (show/hide)»

In the my original Q&A textbook, I posed the following question to physics experts just to test their knowledge of quantum mechanics...

Does flipping the magnetization in an NMR experiment by a full 360° return the system to its original state (i.e., like it was at 0°)? How about two full rotations (720°)?

The answer depends upon one’s definition of “the system” used in the question. If one describes the NMR system by a single wavefunction, the answer is NO for a 360° rotation, but YES for 720°! This unexpected result derives from the spinor property of protons. The spinor property is well known in group theory and is also occurs in solid-state physics where it is referred to as a "crystal double group." In fact the state vectors (|+½> and |-½>) are actually spinors and not simple vectors.

After a rotation of 360° the wave function (Ψ) describing the system can be shown to be identical to that existing at 0°, but with a reversal in its sign. In terms of the wave-function analysis previously presented, this is equivalent to saying that after a 360° rotation, a = -a(0) and b = -b(0), where a(0) and b(0) were the values of a and b before the rotation. An additional 360° rotation (720° total) is required to return a and b (and hence Ψ) to their original values. The fact that two complete rotations are required to return the system to its starting point can be likened to a Möbius strip, where one must travel along the strip twice to return to its origin.

In practical MR imaging applications, however, the single wavefunction description of the NMR system is inadequate because the statistical mechanical nature of the NMR system is not taken into account. The system is more properly described by the mixed state density operator which, being composed of the ensemble averaged outer product of the wavefunction corresponding to the system, does not change sign under a 360° rotation. Thus the magnetization of an ensemble of protons (which is the expectation value of a spin operator) will not change sign under a 360° rotation, and will not be directly observable in a conventional MR imaging experiment.

I introduced this curious spinor property to remind everyone of the beauty and complexity of the NMR phenomenon; it also provides stimulating conversation at physics cocktail parties and baffles residents at radiology rounds. The spinor phenomenon plays no role in routine MR imaging, but it can be physically observable, having been demonstrated in several laboratory NMR experiments in which the spin-up and spin-down portions of the wave function have been ingeniously separated.

---

References
     Elster AD, Burdette JH. Questions and Answers in MRI, 2nd ed. St. Louis: Mosby, 2001, p 28.
     Hanson L. Is quantum mechanics necessary for understanding magnetic resonance?  Concepts Mag Reson Part A 2008;32A(5):329-340.

---

Related Questions
     How do RF-transmit coils work?
     What is net magnetization and how does it apply to NMR? 
     What is meant by flip angle? 
     What is the rotating frame of reference?    

---

←  Previous Question

Next Question  →

↑ Complete List of Questions ↑