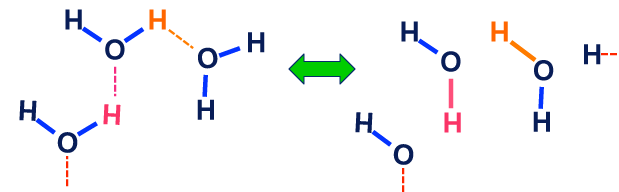
Chemical Exchange
What do you mean by chemical exchange and how does it effect T1 and T2?
|
|
Chemical exchange represents the transfer of a nucleus from one molecular environment to another. Two examples with slightly different features are illustrated below.
In the first case, ¹H on a water molecule exchanges with ¹H on an amide group in the middle of a macromolecule. Here the chemical shift and J-coupling of both ¹H's change as they enter their new molecular environments. Based on bond enthalpies and geometry, the forward and backward rates of this chemical reaction would be relatively slow and unequal, with the equilibrium population states asymmetrically favoring ¹H remaining on the water molecule.
The second example illustrates hydrogen bonding and chemical exchange in water. Here ¹H nuclei are "traded" among various molecules that are chemically indistinguishable but which may have different rotational and translational energies. The expected exchange rates would be quite fast with no preference for one water molecule over another. Because the reactants and products are identical, there would be no change in chemical shift or J-coupling.
In the first case, ¹H on a water molecule exchanges with ¹H on an amide group in the middle of a macromolecule. Here the chemical shift and J-coupling of both ¹H's change as they enter their new molecular environments. Based on bond enthalpies and geometry, the forward and backward rates of this chemical reaction would be relatively slow and unequal, with the equilibrium population states asymmetrically favoring ¹H remaining on the water molecule.
The second example illustrates hydrogen bonding and chemical exchange in water. Here ¹H nuclei are "traded" among various molecules that are chemically indistinguishable but which may have different rotational and translational energies. The expected exchange rates would be quite fast with no preference for one water molecule over another. Because the reactants and products are identical, there would be no change in chemical shift or J-coupling.
Chemical exchange between a water proton and a proton on an amide group in a macromolecule.
|
Hydrogen bonding in water. H nuclei (such as those colored red and orange above) form bridges (dotted lines) with nearby oxygen atoms and transfer molecules. |
Although chemical exchange is generally thought of as involving the physical transfer of nuclei between two molecules, several equivalent processes without frank nuclear transfer exist. For example, the molecule where the proton resides may simply change its conformation (such as going from a cis- to a trans- state). A second example commonly seen in biological tissues is where an intact molecule moves or is transported between different compartments (such as from inside to outside of a cell). A final example is where an intact molecule goes from a free to a bound state (such as when free water molecules become restricted in their motion along a protein hydration layer.)
|
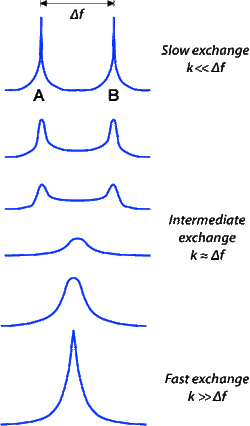
The effects of chemical exchange on the Bloch equations were first modeled by McConnell and later extended by Forsén and Hoffman in the 1950s and 1960s. The simplest case is a reversible exchange of an ¹H proton between two molecules (A ↔ B) separated by a chemical shift frequency (Δf) and governed by a single reaction rate (k).
Reaction rates can vary from nanoseconds to many seconds, depending on the system studied. If the exchange rate is slow on the chemical shift time scale (k<<Δf), two sets of signals are observed. For fast exchange rates (k>>Δf) only one signal is observed at an average frequency corresponding to the relative populations of the two chemical species. At intermediate exchange rates (k≈Δf) very large spectral line widths (corresponding to very short T2 values) occur. |
Spectra for spins in two different molecules (A and B) as a function of reaction rate (k) and chemical shift (Δf).
|
More complicated models including multiple molecular environments with different and asymmetric exchange rates have been developed. The results are not intuitively obvious, but can be calculated numerically under various assumptions. As a rule, most of the chemical exchange mechanisms result in a field-dependent shortening of both T1 and T2, with typically a much greater effect on T2. Chemical exchanges occurring over time frames longer than T1 do not generally affect spectral lines widths or the MR signal.
References
Forsén S, Hoffman RA. Study of moderately rapid chemical exchange reactions by means of nuclear magnetic double resonance. J Chem Phys 1963;39:2892-2901.
McConnell HM. Relaxation rates by nuclear magnetic resonance. J Chem Phys 1958; 28:430-1.
Millet O, Loria JP, Kroenke CD et al. The static magnetic field dependence of chemical exchange linebroadening defines the NMR chemical shift time scale. J Am Chem Soc 2000; 122:2867-2877
Spencer RGS, Fishbein KW. Measurement of spin–lattice relaxation times and concentrations in systems with chemical exchange using the one-pulse sequence: breakdown of the Ernst model for partial saturation in nuclear magnetic resonance spectroscopy. J Magn Reson 2000; 142:120–135.
Zimmerman JR, Brittin WE. Nuclear magnetic resonance studies in multiple phase systems: lifetime of a water molecule in an adsorbing phase on silica gel. J Phys Chem 1957; 61:1328-1333.
Forsén S, Hoffman RA. Study of moderately rapid chemical exchange reactions by means of nuclear magnetic double resonance. J Chem Phys 1963;39:2892-2901.
McConnell HM. Relaxation rates by nuclear magnetic resonance. J Chem Phys 1958; 28:430-1.
Millet O, Loria JP, Kroenke CD et al. The static magnetic field dependence of chemical exchange linebroadening defines the NMR chemical shift time scale. J Am Chem Soc 2000; 122:2867-2877
Spencer RGS, Fishbein KW. Measurement of spin–lattice relaxation times and concentrations in systems with chemical exchange using the one-pulse sequence: breakdown of the Ernst model for partial saturation in nuclear magnetic resonance spectroscopy. J Magn Reson 2000; 142:120–135.
Zimmerman JR, Brittin WE. Nuclear magnetic resonance studies in multiple phase systems: lifetime of a water molecule in an adsorbing phase on silica gel. J Phys Chem 1957; 61:1328-1333.
Related Questions
How can you predict the T1 and T2 values of different tissues?
What are the causes of T1 and T2 relaxation?
How can you predict the T1 and T2 values of different tissues?
What are the causes of T1 and T2 relaxation?