Dipole-Dipole Interactions
Can you explain a little more about the dipole-dipole interaction? I still don't quite understand.
|
|
|
The concept of the magnetic dipole has been introduced in a prior Q&A. In brief, protons, electrons, and NMR-active nuclei can be thought of as tiny magnets with north and south poles ("dipoles") whose electromagnetic fields interact through space. This interaction is called a dipole-dipole interaction is the most important single mechanism responsible for T1 and T2 relaxation in biological tissues.
|
A spinning particle (proton, electron, or whole nucleus) modeled as a "dipole" that generates its own local magnetic field.
|
Four major factors determine the strength of the dipolar interaction: (1) types of spins; (2) the distance between them; (3) the angle between them; and (4) their relative motion.
|
Types of spins: Dipole-dipole interactions may be either proton-proton or proton-electron. Due to its small size, an electron has a much larger gyromagnetic ratio (γ) than a proton and so a proton-electron dipolar interaction is much more powerful than a proton-proton interaction. This is the reason paramagnetic substances like Gd+3 with multiple unpaired electrons are so effective at inducing magnetic relaxation.
|
"Through-space" Interaction of magnetic fields from two spinning particles via the dipole-dipole mechanism. |
Distance: The strength of the dipolar interaction depends on the distance between the spins. The effect is inversely proportional to the sixth power of distance (1/r6), explaining why short-range intramolecular dipole-dipole interactions are more powerful than long-range intermolecular ones. This generally means that two ¹H nuclei must approach within about 0.3 nm of each other to be effective at dipole-dipole interactions. If one of the dipoles is an electron or paramagnetic ion, then the distances up to 1 nm may still be effective. In pure water it is estimated that about 70% of the dipolar interactions are intramolecular while 30% are intermolecular.
Angle: The strength of the dipolar interaction also depends on the quantity (3 cos²θ −1), where θ is the angle between the two spins. This leads to the interesting property that the static component of dipole-dipole interaction vanishes when θ ≈ 54.7°. This is the so-called magic angle, the value of θ that makes the term (3 cos²θ −1) = 0. This phenomenon affects primarily T2 relaxation and explains why portions of tendons, nerves, and cartilage may have paradoxically high signal on routine musculoskeletal MR imaging if they make an angle of 54.7° with the main magnetic field. The details of this magic angle phenomenon will be described in a subsequent Q&A.
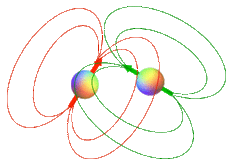
Relative motion: How the spins move relative to one another is a strong determinant of the degree and type of relaxation (combined T1/T2 or T2 alone). If one of the spins resides on a molecule that is tumbling or rotating at frequency ω, its associated dipolar field will also fluctuate at the same frequency. If that frequency happens to closely match the Larmor frequency, then conditions are optimal to cause T1 relaxation in a nearby spin. Conversely, if the molecule on which the spin resides is hardly moving at all (as in large molecules fixed in cell membranes) the dipolar field will be relatively static, producing dephasing of nearby spins and predominantly T2 relaxation.
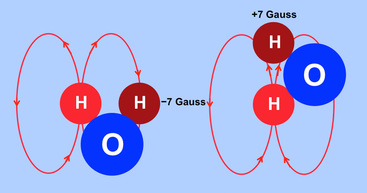
A qualitative appreciation of how molecular motion of a dipolar pair causes locally fluctuating fields can be seen by considering the rotation of a water molecule (HOH) in the diagrams below. Each ¹H nucleus is a dipole generating its own localized magnetic field. The magnitude of such local fields are quite small, on the order of ±7 gauss over typical intramolecular distances of 0.2-0.3 nm.
As the molecule rotates these local fields interact with one another. For ease of explanation let us assume that the light red ¹H nucleus remains stationary as the dark red ¹H nucleus rotates around it. As it rotates the dark red ¹H nucleus experiences a local field that fluctuates by ±7 gauss. The frequency of this local field fluctuation is directly related to the rate of molecular rotation.
A qualitative appreciation of how molecular motion of a dipolar pair causes locally fluctuating fields can be seen by considering the rotation of a water molecule (HOH) in the diagrams below. Each ¹H nucleus is a dipole generating its own localized magnetic field. The magnitude of such local fields are quite small, on the order of ±7 gauss over typical intramolecular distances of 0.2-0.3 nm.
As the molecule rotates these local fields interact with one another. For ease of explanation let us assume that the light red ¹H nucleus remains stationary as the dark red ¹H nucleus rotates around it. As it rotates the dark red ¹H nucleus experiences a local field that fluctuates by ±7 gauss. The frequency of this local field fluctuation is directly related to the rate of molecular rotation.
The local magnetic field near a hydrogen nucleus varies by ± 7 gauss (G) according to location.
|
Dark red hydrogen nucleus experiences a magnetic field fluctuation of ±7G at a frequency determined by the molecular tumbling rate.
|
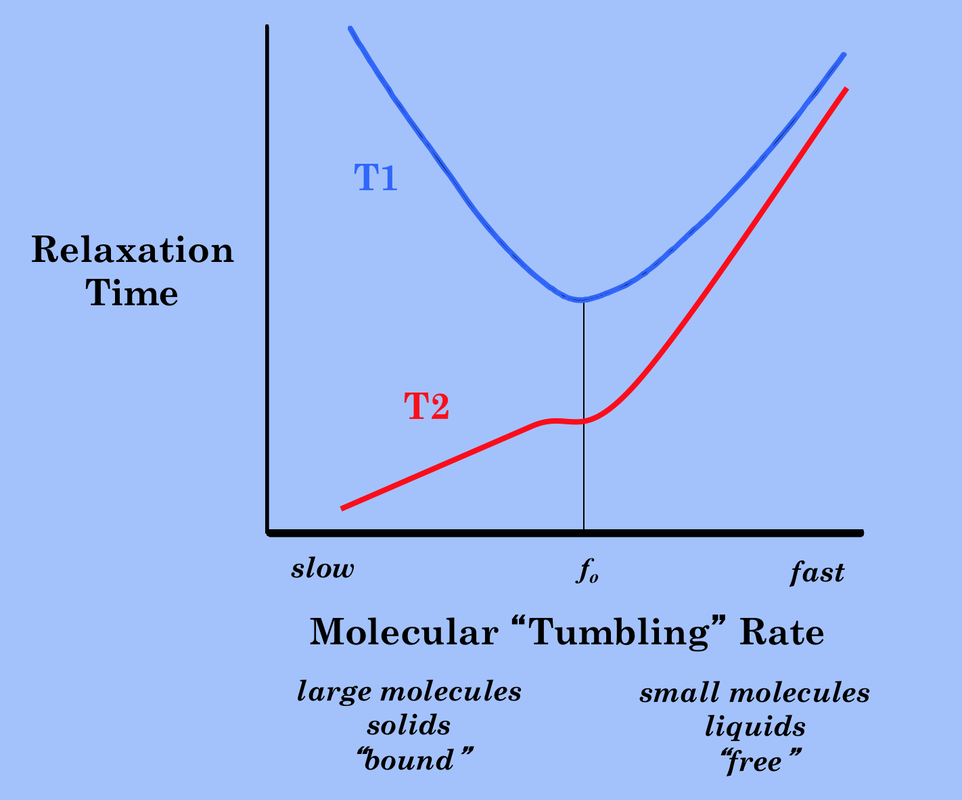
T1 relaxation is most efficient at Larmor frequency (fo).
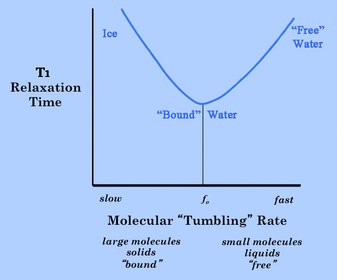
T1 Relaxation Effect. When this molecular "tumbling" rate is close to the Larmor frequency (fo), then the fluctuating magnetic field from one spin is optimal for inducing T1 relaxation in the other. The relationship between T1 and molecular tumbling rate is illustrated to the right.
In this figure we see that water, with its small molecular size, tumbles much too rapidly in its free state to be effective at T1 relaxation. T1 values are longer for free water than for any other substance in the body (approximately 4000 ms at 1.5T). When the water is in a partially bound or in a restricted state, however, its tumbling may be slowed to a rate much closer to the Larmor frequency. Water molecules with restricted motion frequently occur in biological systems where their molecular motion is slowed by interaction with polar amide and hydroxyl groups on the surfaces of macromolecules. The T1 value of "bound" or "structured" water is therefore much shorter than that of free water (typically about 400-800 ms at 1.5T). This is the type of water whose signal we primarily measure when imaging solid organs like the liver or brain.
For completeness the graph shows that as molecular rotation rates slow below the Larmor frequency, the fluctuating dipolar fields are no longer efficient at inducing relaxation and T1 values again increase. If we measured the T1 value of ice, for example, as might form during a cryoablation procedure, we would find it to be very several seconds or more. Ice has extremely long T1 values because in the crystalline state its molecular motions are much slower than the Larmor frequency. Certain (non-biologic) solid crystals have been reported to have T1 values of weeks to months!
In this figure we see that water, with its small molecular size, tumbles much too rapidly in its free state to be effective at T1 relaxation. T1 values are longer for free water than for any other substance in the body (approximately 4000 ms at 1.5T). When the water is in a partially bound or in a restricted state, however, its tumbling may be slowed to a rate much closer to the Larmor frequency. Water molecules with restricted motion frequently occur in biological systems where their molecular motion is slowed by interaction with polar amide and hydroxyl groups on the surfaces of macromolecules. The T1 value of "bound" or "structured" water is therefore much shorter than that of free water (typically about 400-800 ms at 1.5T). This is the type of water whose signal we primarily measure when imaging solid organs like the liver or brain.
For completeness the graph shows that as molecular rotation rates slow below the Larmor frequency, the fluctuating dipolar fields are no longer efficient at inducing relaxation and T1 values again increase. If we measured the T1 value of ice, for example, as might form during a cryoablation procedure, we would find it to be very several seconds or more. Ice has extremely long T1 values because in the crystalline state its molecular motions are much slower than the Larmor frequency. Certain (non-biologic) solid crystals have been reported to have T1 values of weeks to months!
|
T2 Relaxation Effect. As the rate of molecular rotation falls below the Larmor frequency, local fields created by each spin fluctuate less and less and assume an increasingly static character. The z-component of a slowly fluctuating field (Bμz) from one dipole (μ) augments or subtracts from the main field (Bo) at the site of the other dipole. The second dipole then precesses at a slightly lower or higher frequency, gaining or losing phase in the process. This mechanism of dipolar interaction results in T2 relaxation without T1 relaxation. As the solid state is attained, all molecular rotations and translations largely cease and so the static mechanism predominates, resulting in very short T2 values.
|
The z-component from one dipole (Bμz) adds to the Bo field at the second dipole, changing its precession frequency slightly. This results in T2 relaxation.
|
|
The combined graph to the left shows how T2 relaxation time varies as a function of molecular tumbling rate. As expected, T2 becomes very short as the solid state is approached. The small plateau in the T2 curve (accentuated in the diagram for didactic purposes) at the Larmor frequency represents the effect of T1 on T2 relaxation.
|
References
Bloembergen N, Purcell EM, Pound RV. Relaxation effects in nuclear magnetic resonance absorption. Phys Rev 1948;73(7):679-712. (The classic paper where the concepts of spin-lattice and spin-spin relaxation are developed formally as well as the recognition of inhomogeneity effects that we now call T2* but which the authors called T2').
Solomon I. Relaxation processes in a system of two spins. Phys Rev 1955; 99(1):559-565.
Bloembergen N. Spin relaxation processes in a two-proton system. Phys Rev 1956;104(6):1542-1547.
Bloembergen N, Morgan LO. Proton relaxation times in paramagnetic solutions. Effects of electron spin relaxation. J Chem Phys 1961; 14(3):842-850. This paper adds in paramagnetic effects.
Goldman M. Formal theory of spin-lattice relaxation. J Magn Reson 2001; 149:160-187. (Heavy paper for advanced physicists only, but this has everything in it).
Bloembergen N, Purcell EM, Pound RV. Relaxation effects in nuclear magnetic resonance absorption. Phys Rev 1948;73(7):679-712. (The classic paper where the concepts of spin-lattice and spin-spin relaxation are developed formally as well as the recognition of inhomogeneity effects that we now call T2* but which the authors called T2').
Solomon I. Relaxation processes in a system of two spins. Phys Rev 1955; 99(1):559-565.
Bloembergen N. Spin relaxation processes in a two-proton system. Phys Rev 1956;104(6):1542-1547.
Bloembergen N, Morgan LO. Proton relaxation times in paramagnetic solutions. Effects of electron spin relaxation. J Chem Phys 1961; 14(3):842-850. This paper adds in paramagnetic effects.
Goldman M. Formal theory of spin-lattice relaxation. J Magn Reson 2001; 149:160-187. (Heavy paper for advanced physicists only, but this has everything in it).
Related Questions
Does the net magnetization (M) just instantly appear?
When a group of spins is driven into higher energy levels by the action of an RF field, why don't these spins immediately release the absorbed energy and drop back to their original lower energy states?
Does the net magnetization (M) just instantly appear?
When a group of spins is driven into higher energy levels by the action of an RF field, why don't these spins immediately release the absorbed energy and drop back to their original lower energy states?