Causes of Relaxation
What are the causes of T1 and T2 relaxation?
|
|
In the approximately 70 years since Bloch's original description, considerable progress has been made in explaining the physical mechanisms responsible for T1 and T2 relaxation. We now have reasonably comprehensive theories that explain relaxation in water, simple solutions of salts and proteins, paramagnetic ions, and relatively homogenous solid materials (such as collagen, lipids, and macromolecules).
|
Biological tissues, however, are infinitely more complex, with internal microstructures containing water and larger molecules distributed nonuniformly and within compartments. As such, no comprehensive quantitative theory has yet been developed that easily explains, for example, why liver or brain have the specific T1 and T2 values that they do. Nevertheless, much insight can still be gained by understanding the six basic mechanisms responsible for relaxation in simpler substances.
|
PRINCIPAL RELAXATION MECHANISMS |
Below are very brief summaries of the major mechanisms underlying T1 and T2 relaxation. These will be more completely flushed out in subsequent Q&A's.
Dipole-Dipole Interaction: The dominant mechanism for ¹H relaxation
|
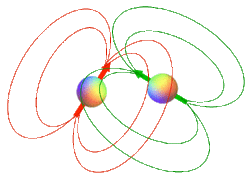
As described in a previous Q&A the electromagnetic field from a particle can be considered to emanate from an idealized tiny bar magnet with north and south poles (the "dipole"). For our purposes the term dipole is synonymous with either a nucleus (proton) or an unpaired electron. A dipole-dipole interaction is a "through space" interaction of the fields from two such spinning particles. If the spins reside on the same molecule it is called an intramolecular dipolar interaction; if on different molecules an intermolecular interaction.
|
Through-space interaction of the magnetic fields of two nearby "dipoles" (protons or electrons). Static field distortions contribute to T2 relaxation. Molecular motion of each spin near the Larmor frequency causes local magnetic field fluctuations with both T1 and T2 relaxation.
|
The effectiveness of a dipole-dipole interaction at producing relaxation depends on 1) the types of spins; 2) their spatial relationship; and 3) their relative motion. Electrons are more powerful at inducing relaxation than protons, so proton-electron (or ion) interactions result in much greater relaxation than proton-proton interactions. The dipolar interaction scales inversely with the sixth power of distance between the dipoles; so intramolecular interactions are much more effective than intermolecular ones. Finally, molecular motion (primarily rotation rates) of the dipoles compared to the Larmor frequency determines the degree of relaxation and whether T1 or T2 effects predominate. All of these ideas will be more completely explored in several later Q&A's.
Chemical Shift Anisotropy
|
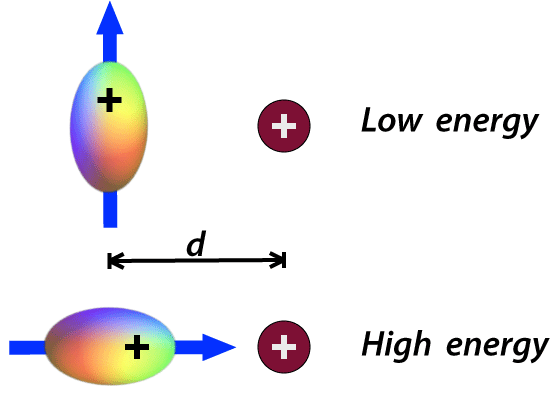
Electron clouds in molecules provide shielding of nuclei from the full intensity of an externally applied magnetic field (Bo). The resonance frequencies of ¹H nuclei will vary slightly depending on shielding in their local molecular environments. This is known as a chemical shift and forms the basis for MR Spectroscopy.
|
Electron clouds provide variable shielding of nuclei from the effects of the external field (Bo). Electronegative atoms (like oxygen) attract electrons deshielding other atoms. The resonance frequencies of different nuclei vary slightly depending on their local molecular environments.
|
Chemical shift depends upon the orientation of the molecule relative to Bo. If the chemical shift varies significantly in different directions, chemical shift anisotropy (CSA) is said to exist. If the molecule is rapidly tumbling (in solution, for example), directional asymmetries average out and CSA is not important. If the molecule is restricted in its motion (such as water complexed to a macromolecule), then CSA effects may be important. This phenomenon could partially explain the paradoxically shorter T2 values observed in biological tissues than would be predicted from their molecular rotation rates alone. CSA also explains the short T2 of tendons which are composed of Type I collagen oriented in parallel bundles. CSA relaxation scales with the square of field strength (Bo²), so is more important at higher fields. It is also important in the imaging and spectroscopy of the phosphorus (³¹P) nucleus that has exceptionally large chemical shifts relative to its resonance frequency.
Molecular Translation / Flow / Diffusion
|
Any physical process that causes a molecule to move between different local environments during the course of an MR experiment can result in relaxation. The displacement may be due to translation of the molecule by a chemical, electrical, or gravitational gradient. It might be an organized, en masse displacement of many molecules, as in blood or CSF flow. Or it might be an entirely random process due to microscopic diffusion, the thermally-induced displacements of molecules due to Brownian motion.
|
Diffusion of water molecules through a local magnetic field gradient due to a susceptibility disturbance.
|
If the external magnetic field through which a translating (or flowing or diffusing) molecule is uniform, then the nucleus' resonance frequency will remain constant and no relaxation will occur. If the external field is not uniform, however, then the nucleus will resonate at different frequencies and develop a random phase shifts as it moves, resulting in loss of transverse coherence. Such local field nonuniformities are typically due to susceptibility-generated gradients on a macroscopic (e.g., near metallic foreign bodies or air-tissue interfaces) or microscopic (e.g due to paramagnetic ions, microcalcifications, or hemosiderin deposits) basis. Translation/flow/diffusion results primarily in T2 relaxation proportional to the square of the gradient field and the length of time the spin moves within that gradient.
It should be noted that in MR Angiography (MRA) and Diffusion-Weighted Imaging (DWI), additional external strong gradients are often applied to create enhanced sensitivity to flow or diffusion. These external gradients are not considered causes of true-T2 relaxation since they do not derive from intrinsic, natural processes and have no effect on stationary spins.
Chemical Exchange
Chemical exchange
Hydrogen atoms are frequently involved in chemical exchange processes, wherein they are physically transferred from one molecule to another. Alternatively, the hydrogen proton may undergo a "chemical exchange equivalent" by residing on a molecule that changes its structure or moves between chemically different compartments in a tissue (e.g., from inside to outside of a cell). Relaxation rates produced by chemical exchange processes are proportional to the square of the applied magnetic field.
|
Scalar (J)-Coupling
Scalar- or J-Coupling is an interaction of two nuclear spins on the same molecule transmitted through distortions in electron clouds. This contrasts with dipole-dipole interactions that occur via direct electromagnetic interactions "through space" and do not require an electron cloud intermediary. |
Scalar (J)-coupling interaction between two nuclei is mediated by the electron clouds they share.
|
Overall J-coupling plays a relatively minor role in determining the overall relaxation properties of tissues. It is independent of field strength and generally has a much larger effect on T2 than T1 relaxation. Some of its effects can be seen in clinical MR, however. For example, J-coupling interactions are responsible for the splitting of chemical peaks (such as the famous lactate doublet) seen in MR Spectroscopy. Additionally, J-coupling is responsible for a time-dependent modulation of the MR signal from fat on spin-echo images.
|
Electric-Quadrupole Coupling
Quadrupolar coupling is an extremely powerful and the dominant relaxation mechanism for nuclei (such as ²³Na) with spin quantum numbers (I) > ½. Such nuclei possess nonspherical charge distributions (quadrupolar moments). They interact powerfully with electric (rather than magnetic) field gradients in surrounding electron clouds, resulting in unequal splitting of the quadrupolar energy levels. I = ½ nuclei like ¹H have spherical charge distributions so do not relax by this mechanism. |
Nuclei with I ≥ 1 have a nonspherical (ellipsoidal) charge distribution and interact with nearby electrical fields. Even though the mean distance (d) between the quadrupolar nucleus and the lone charge (+) does not change, nuclear orientation effects the energy levels and causes relaxation.
|
References
Bloembergen N, Purcell EM, Pound RV. Relaxation effects in nuclear magnetic resonance absorption. Phys Rev 1948;73(7):679-712. (The classic paper where the concepts of spin-lattice and spin-spin relaxation are developed formally as well as the recognition of inhomogeneity effects that we now call T2* but which the authors called T2').
Carr HY, Purcell EM. Effects of diffusion on free precession in nuclear magnetic resonance experiments. Phys Rev 1954;94(1):630-8. (Although Hahn described the effects of diffusion on spin-echoes four years previously, this paper takes the concept a step further).
Hahn EL. Spin echoes. Phys Rev 1950;80(4):580-594. (A "must-read". This paper has it all. Hahn was just a graduate student when he wrote this!)
Simpson JH, Carr HY. Diffusion and nuclear spin relaxation in water. Phys Rev 1958;111(5):1201-2. (Shows that in water at physiological temperatures T1 ∝ Diffusion constant (D) ∝ Temperature)
Torrey HC. Bloch equations with diffusion terms. Phys Rev 1956;104(1):563-5.
Bloembergen N, Purcell EM, Pound RV. Relaxation effects in nuclear magnetic resonance absorption. Phys Rev 1948;73(7):679-712. (The classic paper where the concepts of spin-lattice and spin-spin relaxation are developed formally as well as the recognition of inhomogeneity effects that we now call T2* but which the authors called T2').
Carr HY, Purcell EM. Effects of diffusion on free precession in nuclear magnetic resonance experiments. Phys Rev 1954;94(1):630-8. (Although Hahn described the effects of diffusion on spin-echoes four years previously, this paper takes the concept a step further).
Hahn EL. Spin echoes. Phys Rev 1950;80(4):580-594. (A "must-read". This paper has it all. Hahn was just a graduate student when he wrote this!)
Simpson JH, Carr HY. Diffusion and nuclear spin relaxation in water. Phys Rev 1958;111(5):1201-2. (Shows that in water at physiological temperatures T1 ∝ Diffusion constant (D) ∝ Temperature)
Torrey HC. Bloch equations with diffusion terms. Phys Rev 1956;104(1):563-5.