Whole and Half Integers for I
Why are the allowable values for spin either whole or half integers? Why couldn't all the spins be whole numbers, or for that matter, any value whatsoever?
|
|
The fundamental tenet of quantum mechanics is that many basic phenomena at the atomic level (such as energy emission and angular momentum) appear to be quantized. “Quantized” means that when certain properties of a system are measured, a continuous range of results are not observed, but rather a set of discrete (separate) values. If “quanta” come in discrete units then it makes sense to count them with integers.
The idea of a spin = ½ particle was at first met with skepticism by much of the scientific community. It was not until 1928 when Paul Dirac directly derived this result for the electron from relativistic quantum mechanics that half-integer quantum numbers became widely accepted.
The idea of a spin = ½ particle was at first met with skepticism by much of the scientific community. It was not until 1928 when Paul Dirac directly derived this result for the electron from relativistic quantum mechanics that half-integer quantum numbers became widely accepted.
|
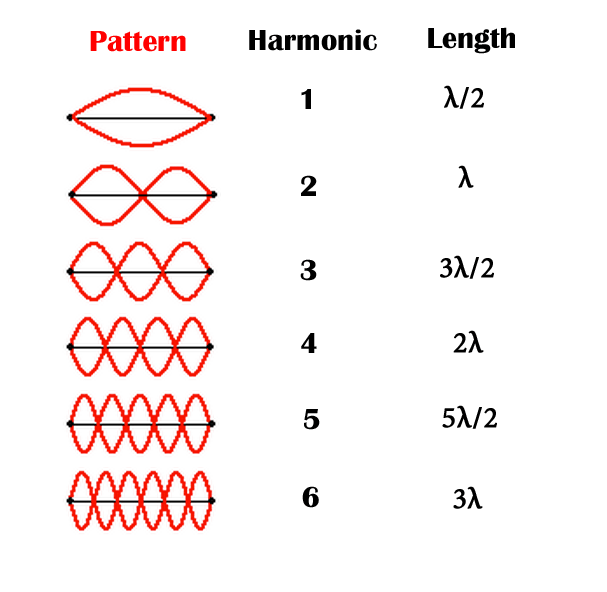
Some appreciation for why both integer and half-integer quantum numbers crop up may be gained by considering the properties of simple standing waves, such as vibrations of a guitar string. It is well recognized that standing waves only occur when their harmonics are either whole or half-integral multiples of the string length.
The guitar string example is only an analogy, not a proof, of why both whole and half-integer spin values might be reasonable at the quantum level. I present this to provide you with some comfort that all quantum features are not entirely foreign to our experience in the macroscopic world. |
Harmonic vibrations of a string follow a progression of wavelengths (λ) similar to spin quantum numbers: 1/2, 1, 3/2, 2, 5/2, etc.
|
References
Wolfe J. Music Acoustics: Strings, standing waves, and harmonics (link). Sydney: University of New South Wales (accessed 2014)
Wolfe J. Music Acoustics: Strings, standing waves, and harmonics (link). Sydney: University of New South Wales (accessed 2014)
Related Questions
What is spin?
How do you predict the value of nuclear spin (I) based on the number of protons and neutrons?
What is the difference between "spin" and "spin state"?
What is spin?
How do you predict the value of nuclear spin (I) based on the number of protons and neutrons?
What is the difference between "spin" and "spin state"?