Noise in PI
Why do parallel imaging studies look so noisy?
|
|
Parallel imaging (PI) studies can indeed look "noisy" at times. This is a direct consequence of the fact that the primary purpose of PI techniques is to reduce imaging time. In so doing, fewer data points are acquired and averaged, so the signal-to-noise ratio (SNR) correspondingly decreases. The SNR of PI sequences is therefore always lower than that of equivalent non-PI sequences.
The SNR of PI sequences are affected by all of the same factors that affect non-PI sequences: field strength, magnet hardware, coil loading, tissue imaged, pulse sequence, pulse sequence timing parameters, voxel volume, number of phase-encoding steps, receiver bandwidth, number of signals averaged, etc. Additionally, the SNR for PI sequences (SNRparallel) are further reduced by two additional factors as reflected in the equation below
where R is the parallel imaging reduction or acceleration factor and g is a spatially dependent term called the geometry factor.
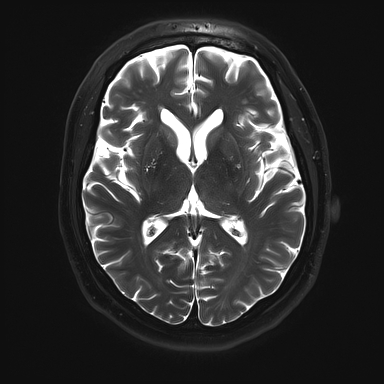
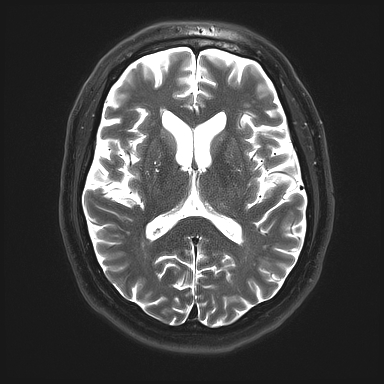
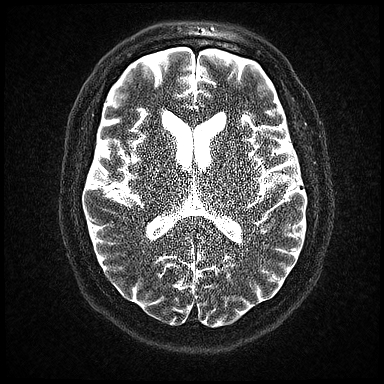
The √R term represents the expected SNR loss resulting from reducing scan time by a factor of R. Since only 1/R of the k-space lines are sampled, this term has the similar effect to reducing the number of phase encoding steps or signal averages would have on SNR for a non-PI sequence. Hence, selecting R=2 reduces imaging time by 1/2 and decreases SNR by 1/√2 ≈ 0.71. The significant impairment of SNR is seen in the images below, where R is increased from 1 to 3 to 6.
No acceleration (R=1)
|
Acceleration factor R=3
|
Acceleration factor R=6
|
SENSE knee MRI with R=4. Note non-uniformdistribution of noise across the image
related to a spatially varying g-factor.
The geometry factor, g, is more interesting, and unique to PI. It depends on the number of aliased replicates for each point and their associated differences in coil sensitivities. The g-factor is not a constant, but varies by location across the image. With typical coil designs in common use, g-factors ranging from 1.0 to 2.0 across the imaging volume are common.
The g-factor thus depends on 1) number and location of surface coils, 2) coil loading, 3) plane of imaging, 4) direction of phase-encoding within the scan plane, and 5) voxel location within the imaged region. It relates to the number, size, orientation of surface coil elements and can be thought of as a measure of coil separation. It is also sometimes called the "noise amplification factor."
The g-factor thus depends on 1) number and location of surface coils, 2) coil loading, 3) plane of imaging, 4) direction of phase-encoding within the scan plane, and 5) voxel location within the imaged region. It relates to the number, size, orientation of surface coil elements and can be thought of as a measure of coil separation. It is also sometimes called the "noise amplification factor."
References
Aja-Fernandez, Vegas-Sanchez-Ferrero G, Tristan-Vega A. Noise estimation in parallel MRI: GRAPPA and SENSE. Magn Reson Imaging 2014; 32:281-290.
Breuer FA, Kannengiesser SA, Blaimer M, Seiberlich N, Jakob PM, Griswold MA. General formulation for quantitative g-factor calculation in grappa reconstructions. Magn Reson Med 2009; 62:739–46.
Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: Sensitivity encoding for fast MRI. Magn Reson Med 1999; 42:952-962.
Robson P, Grant A, Madhuranthakam A, Lattanzi R, Sodickson D, McKenzie C. Comprehensive quantification of signal-to-noise ratio and g-factor for image-based and k-space-based parallel imaging reconstructions. Magn Reson Med 2008; 60:895.
Sodickson DK, Griswold MA, Jakob PM, et al. Signal-to-noise ratio and signal-to-noise efficiency in SMASH imaging. Magn Reson Med 1999; 41:1009-1022.
Aja-Fernandez, Vegas-Sanchez-Ferrero G, Tristan-Vega A. Noise estimation in parallel MRI: GRAPPA and SENSE. Magn Reson Imaging 2014; 32:281-290.
Breuer FA, Kannengiesser SA, Blaimer M, Seiberlich N, Jakob PM, Griswold MA. General formulation for quantitative g-factor calculation in grappa reconstructions. Magn Reson Med 2009; 62:739–46.
Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: Sensitivity encoding for fast MRI. Magn Reson Med 1999; 42:952-962.
Robson P, Grant A, Madhuranthakam A, Lattanzi R, Sodickson D, McKenzie C. Comprehensive quantification of signal-to-noise ratio and g-factor for image-based and k-space-based parallel imaging reconstructions. Magn Reson Med 2008; 60:895.
Sodickson DK, Griswold MA, Jakob PM, et al. Signal-to-noise ratio and signal-to-noise efficiency in SMASH imaging. Magn Reson Med 1999; 41:1009-1022.
Related Questions
Are there any artifacts specific to parallel imaging?
Are there any artifacts specific to parallel imaging?