Phase Coherence

Why are all the spins brought into phase with one another after a 90°-pulse?  I don't understand why this should happen.  

In spite of what you may have been told or read, THIS DOES NOT HAPPEN!  The 90°-pulse only brings a tiny fraction (not all) of the spins into transverse phase coherence with one another.  And these newly in-phase spins are the same ones that were originally preferentially aligned with the Bo field before the RF-pulse.

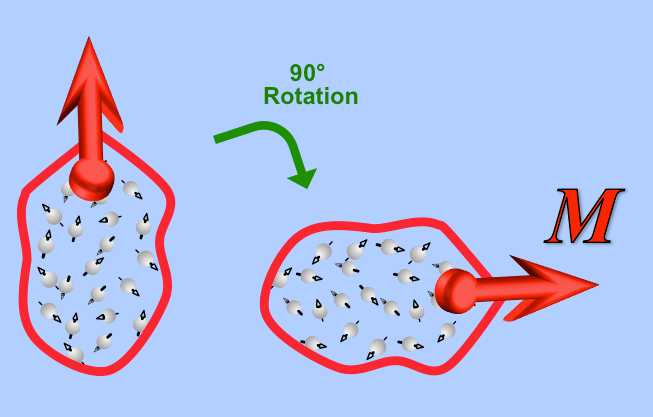
It can be shown by relatively straightforward quantum mechanical arguments that a homogeneous RF-field can never change the relative orientations of non-interacting spins. An RF-field can only rotate the spin system as a whole (and thus its net magnetization, M).

The best way to understand this difficult concept, I believe, is to return to an analogy used in a prior Q&A, "Compasses in a Dryer".  

Compasses in the Dryer Analogy

A 90°-pulse rotates the entire spin system including M into the transverse plane. The mild thermodynamic "order" that exists in the longitudinal direction before the pulse is reflected in the transverse plane as a mild form of "coherence."

In this analogy, individual spinning nuclei were likened to tiny compass needles each seeking to point to the north pole (symbolized by the North Star, Polaris). Because of thermal interactions (the dryer rotating), the individual compass needles ended up pointing in all possible directions. On the average, however, more were pointing north than in any other direction. When we summed them all together, we obtained M, the net magnetization (technically, a statistical "expectation") that pointed due North.

At equilibrium prior to the RF-pulse the spin system has a net population difference representing a form of thermodynamic "order". The only effect of the 90°-pulse is to rotate this entire spin-distribution including M into the transverse plane. Thus what was a slightly skewed spin energy distribution in the longitudinal direction has become "phase coherence" in the transverse plane after the RF-pulse.

After the 90°-pulse only a small fraction of spins are actually "pointing" in the M direction. The phases of the million+ other spins are all randomly dispersed and cancel each other out, so only the few "coherent" ones contribute to vector M. 

Advanced Discussion (show/hide)»

From a quantum mechanical perspective, recall from a previous Q&A that the wave function describing the hydrogen nucleus could be written as:

Ψ(t) = a |+½> + b |-½>

where a and b are time-dependent quantum amplitudes incorporating "harmonic oscillations" of the two principal states |+½> and |-½>.

When an RF field is applied at the Larmor frequency, its action on the wave function Ψ(t) is to induce a "rotation" or mixing of the a and b components while preserving their total amplitudes (|a|² + |b|²). This is the quantum mechanical explanation for why the transverse magnetization after a 90°-pulse is the same as the longitudinal magnetization before the pulse. It is also the reason that this same amount of magnetization, but no more, can be rotated to 180° or any other angle in an NMR fast passage experiment. In an odd sort of way, therefore, the RF-field really does "rotate" the magnetic moment of a proton, but in a manner much more complex and beautiful than the tipping of a spinning top.

---

References
     Elster AD. Questions and Answers in MRI, 1st Ed. St. Louis: Mobsy, 1994, pp. 26-28. 
     Hanson L. Is quantum mechanics necessary for understanding magnetic resonance?   Concepts Mag Reson Part A 2008;32A(5):329-340.

---

Related Questions
     What is net magnetization and how does it apply to NMR? 
    If a system seeks to minimize its total energy level, why don't all the protons simply fall into the lower energy state?   

---

←  Previous Question

Next Question  →

↑ Complete List of Questions ↑