Distribution of Energy States

If a system seeks to minimize its total energy level, why don't all the protons simply reside in the lower energy spin state?  
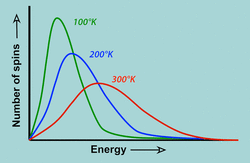
At temperatures close to absolute zero, we would indeed predict that the vast majority of spins would have quantum amplitudes vastly favoring the lower energy ("parallel") state. At body temperatures, however, this tendency for spins to "prefer" the lower energy level is opposed by thermal motions that tend to equalize the two energy levels. The resultant equilibrium distribution is therefore a compromise predicted by the Boltzmann distribution
N+/N− = exp [− ΔE / kT]

where N+ and N- represent the number of spins one would expect to measure in the spin-up and spin-down configurations, ΔE is the difference in energy between the two states, k is the Boltzmann constant (1.381 x 10-23 joules/°K), and T is the absolute temperature in degrees Kelvin. At body temperature in a field of 1.0 Tesla, this equation predicts that the N+ and N- are nearly equal; only a small excess (~3 x 10-6) of spins can be expected to be found in the lower energy (spin-up) state when measured.
Boltzmann distribution, NMR
The Boltzmann distribution shows distribution of particle energies as a function of temperature. Near room/body temperatures (300 °K red curve) the distribution of low and high energy particles is nearly equal.
NMR equilibrium magnetization
"Compasses in a Dryer" Analogy
Another way to think about the distribution of spin states and thermal interactions is using the "Compasses in a Dryer" analogy (pictured left).  Here individual nuclei are envisioned as small compasses placed in a dryer.  Just as nuclei "prefer" to point in the direction of the main magnetic field, so the little compasses all try to align along the earth's magnetic field and point to the North Star. The compasses are all constantly being jarred by the tumbling dryer and interact with each other (the equivalent of thermal collisions and spin-spin interactions experienced by nuclei). As such, only a small fraction of the compasses will actually point north.  
On the average, however, more will point north than any other direction. The net field from all these little compasses summed together is equivalent to the net magnetization vector M. The maximum value of net magnetization at equilibrium along the direction of the main magnetic field (Bo) is denoted Mo. As we will show in later Q&A's, Mo determines the maximum amount of signal it is possible to generate from an NMR/MRI experiment.

Both classical thermodynamic analysis using the Boltzmann distribution or quantum mechanics provides equivalent estimates for the value of Mo 
Mo  ≈  γ² h² Ns Bo / 4kT
where γ is the gyromagnetic ratio, h is Planck's constant, Ns is the number of spins, Bo is magnetic field strength, k is the Boltzmann constant, and T is absolute temperature.  The most important practical conclusion that can be drawn from this equation are that Mo is directly proportional to both the number of spins and to magnetic field strength.  Thus potential MR signal will be greater for substances with larger numbers of available spins ("spin densities") and when performed at higher magnetic fields. 

Advanced Discussion (show/hide)»

References
     Keeler J. NMR and energy levels.  From The Keeler Group, Lectures by James Keeler, 2004 (http://www-keeler.ch.cam.ac.uk/lectures/)
     Hanson L. Is quantum mechanics necessary for understanding magnetic resonance?  Concepts Mag Reson Part A 2008;32A(5):329-340.
Related Questions
     What is the difference between "spin" and "spin state"?
     When a group of spins is driven into higher energy levels by the action of an RF field, why don't these spins immediately release the absorbed energy and drop back to their original lower energy states?