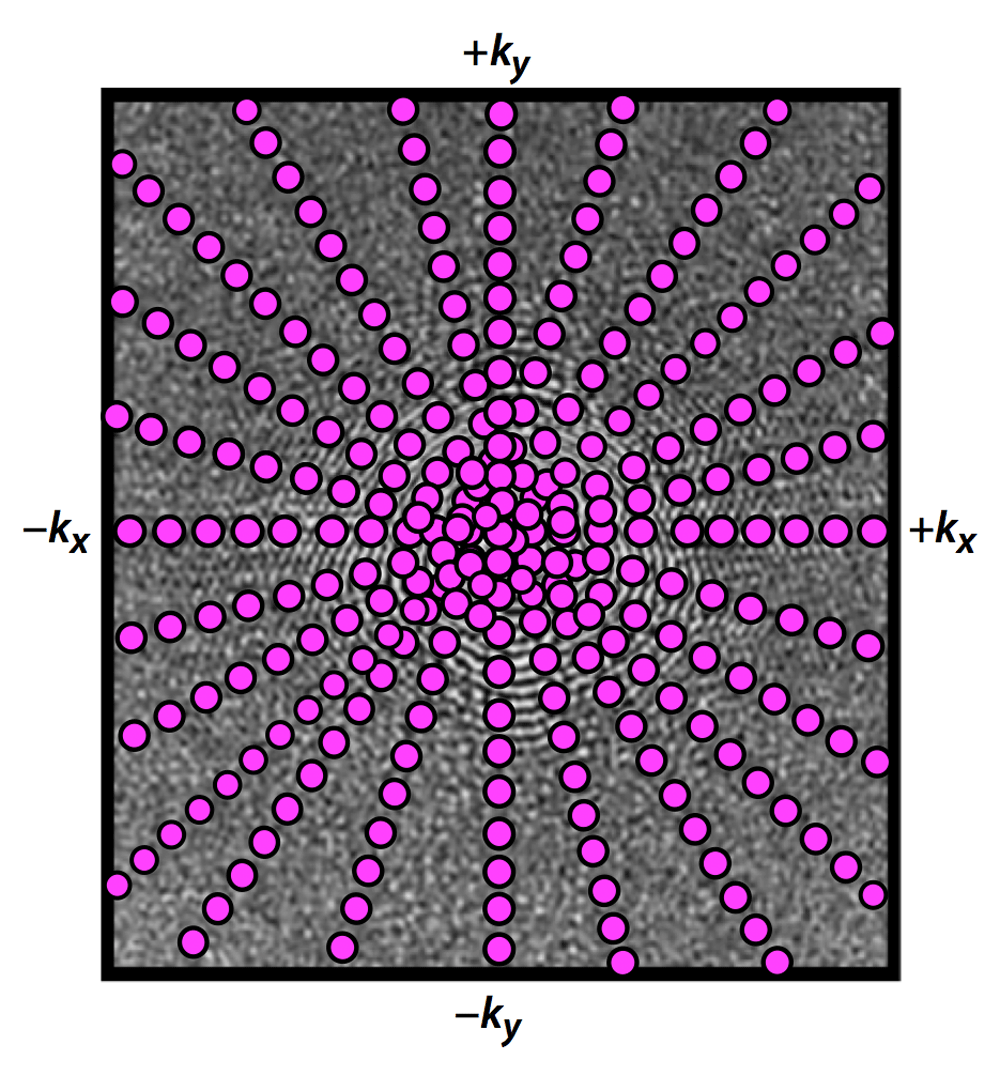
Radial sampling

Why would you want to use a radial  k-space sampling method?  

Radial sampling of k-space data, one of the earliest methods for image reconstruction, was largely supplanted in the 1980's by the "spin-warp" technique that employed rectilinear (Cartesian) data acquisition. To this day, Cartesian methods remain dominant, but radial (and spiral) approaches are fast gaining ground.

Rectilinear (Cartesian) sampling of k-space

Radial sampling of k-space

The principal advantage of Cartesian sampling is that the data elements are regularly spaced and can be placed directly into standard array processors designed for efficient Fast Fourier Transformation (FFT) computations. Radial methods generate data points that do not fall into a rectangular matrix. To efficiently process such non-uniformly acquired data, these points must be morphed into a Cartesian format, an iterative process commonly referred to as "gridding".

The major benefit of radial sampling (leading to its now widespread adoption) is relative insensitivity to motion artifacts. Unlike Cartesian methods, radial sampling does not have unique frequency- and phase-encode directions. Noise from moving anatomic structures thus does not propagate as discrete ghosts along a single phase-encode direction, but is distributed more diffusely across the entire image. 

In radial acquisition the center of k-space is oversampled and continuously updated due to the overlapping "spokes" that repeatedly pass through this region. This redundancy can be exploited to detect and correct for movement if the signal from the k-space center changes between views. Additionally, all radial spokes make equal contributions to the image (unlike Cartesian sampling where just a few lines through the center of k-space set overall image contrast and noise levels). So motion on just one or a few radial views is not likely to severely degrade image quality.

PROPELLER sequence sampling "blades" of data
in a rotating fashion around the center of k-space

​Today's most widely used radial sampling method is GE's PROPELLER (Periodically Rotated Overlapping ParalEL Lines with Enhanced Reconstruction) or one of its variants: Siemens' (BLADE), Philips' (MulitVane), Hitachi's (RADAR), and Canon's (JET).  Instead of a single radial line, a group of several (typically 8-32) parallel lines (called "blades") are collected in a multi-echo acquisition. In clinical practice this is most commonly a 2D Fast/Turbo spin echo (FSE/TSE) sequence. The blades are then rotated about 10°−20° at which time a second set of data are acquired. The process continues until imaging data from the entire k-space circle has been collected. Further information and examples of PROPELLER can be found in this related Q&A.

---

"Stack of Stars"

Primary radial acquisition by sampling of individual lines (rather than groups/blades) is now offered by at least one major vendor. Siemens' StarVIBE product combines in-plane radial sampling using a fat-suppressd spoiled-GRE core sequence.  The process can be extended to 3D, using rectilinear (Cartesian) sampling in the z-direction while maintaining radial sampling in the xy-plane. This 3D implementation is known as Stack of Stars. 

---

Advanced Discussion (show/hide)»

An additional advantage of radial acquisition is that it allows oversampling (512 or greater) in all directions without a time penalty. In conventional (Cartesian) imaging, oversampling is confined to a single direction (frequency-encode or readout). Because radial acquisition occurs in all directions, oversampling is not confined to a single axis. Accordingly, the field of view (FOV) can be smaller than the imaged object in radial sampling scheme without aliasing/wrap-around artifacts.

In addition to the gridding problem, another disadvantage of radial acquisition is uncertainty about the exact location of samples due to gradient delays and distortions. These gradient effects may shift the apparent positions of objects in different directions. To overcome this, a brief calibration scan is typically run prior to performing a radial sequence.

An fascinating mathematical question is how to choose the optimal angles for the radial spokes and in what order to acquire them. One elegant solution is to increment each spoke by approximately 111.25º, which is 180º divided by the golden ratio (Φ = ½(√5+1) ≈ 1.62) from classical geometry. The golden ratio has a variety of interesting properties that explains its presence in nature, including determining the shapes of sea shells and distribution of leaves on plant stems. When the golden angle is selected for a radial acquisition, each successive spoke divides the largest remaining angular gap in half. As the process continues a uniform sampling of k-space is approached in the limit. Symmetrical distribution of spokes occurs when the number of spokes matches one of the Fibonacci numbers (5, 8, 13, 21, 34, 55, etc). A promising application of this method is known as GRASP (Golden-angle RAdial Sparse Parallel) MRI.

---

References
     Block KT, Chandarana H, Milla S, et al. Toward routine clinical use of radial stack-of-stars 3D gradient-echo sequences for reducing motion sensitivity. J Korean Soc Magn Reson Med 2014; 18:87-106.  [DOI LINK]
     Chandarana H, Block TK, Rosenkrantz AB, et al. Free-breathing radial 3D fat-suppressed T1-weighted gradient echo sequence: a viable alternative for contrast-enhanced liver imaging in patients unable to suspend respiration. Invest Radiol. 2011;46:648–653. (StarVIBE and Stack of Stars implementation for liver imaging).
     Feng L, Grimm R, Block KT, et al. Golden-angle radial sparse parallel MRI: combination of compressed sensing, parallel imaging, and golden-angle radial sampling for fast and flexible dynamic volumetric MRI. Magn Reson Med 2014; 72:707-717. (The "GRASP" technique)
     Lauterbur PC. Image formation by induced local interactions: examples employing nuclear magnetic resonance. Nature 1973; 242:190-1. (Historic paper where radial reconstruction was used to produce the world's first MR image).
     Pipe JG. Motion correction with PROPELLER MRI: application to head motion and free-breathing cardiac imaging. Magn Reson Med 1999; 42:963-969.

---

Related Questions
     What about wrap-around artifacts on radial or spiral imaging? it seems like they should always be present because phase-encode goes in every direction. 
     How does PROPELLER reduce motion artifacts? 

---

←  Previous Question

Next Question  →

↑ Complete List of Questions ↑