Dielectric Artifact

What is the dielectric effect and how does it produce artifacts in MRI? 

In MRI we often focus on magnetic fields like Bo and B1, so it is easy to forget that a coexisting electric field (E) is always present. As described by the Maxwell equations, B and E fields oscillate perpendicular to each other and to the direction of wave propagation. When electromagnetic waves encounter the human body, several phenomena occur: 1) the wavelength decreases; 2) electrical currents are generated; and 3) wave reflection/refraction may develop at tissue interfaces. The term dielectric effect refers to the interaction of matter with the E component of an electromagnetic field. 

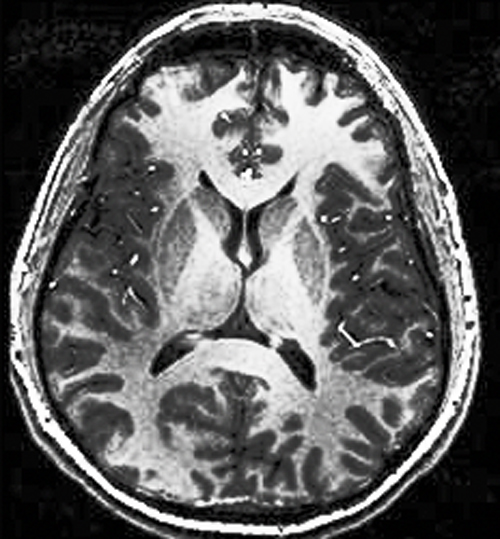
Abnormal bright and dark areas due to B1 field inhomogeneity are frequently noted at very high fields (3T and above). Although the nature of these artifacts is not entirely clear, these are commonly referred to as dielectric artifacts.

"Dielectric" artifact at 7.0T. Center of brain is abnormally brightened.

"Dielectric" artifact at 3.0T. Center of abdomen with ascites is abnormally darkened.

RF wavelengths in tissue as a function of field strength.

The argument that these artifacts are due to dielectric effects is based on considering RF-wavelengths in tissues as a function of field strength. As can be seen in the diagram left, at fields of 1.5T and lower, RF wavelengths are long compared to the size of the body. As the magnetic field is increased, these wavelengths become the same or smaller than the anatomic regions imaged. In theory standing wave currents might arise flowing in opposite directions from two sides of the patient creating a pattern with destructive interference (dark areas) and constructive interference (bright areas) separated by quarter wavelengths. 

The degree to which significant dielectric resonances cause these bright and dark areas remain controversial. The relatively high electrical conductivity of tissues introduces a "skin-depth" term that serves to damp standing wave phenomena. Central brightening has been demonstrated in high-conductivity phantoms where dielectric resonances should be minimal. In summary, dielectric effects and associated artifacts are progressively important as field strength increases, although a simplistic model of dielectric-induced standing waves may only explain a small part of the phenomenon.

Advanced Discussion (show/hide)»

The degree to matter interacts with electric and magnetic fields can be described by three parameters: magnetic permeability (μ), electric permittivity (ε), and electric conductivity (σ). In general these parameters vary with temperature, electromagnetic frequency, and physical state of the matter. Because they may also vary with position and direction they are more accurately represented as vectors (tensors) rather than scalar quantities. Nevertheless, for simplicity of explanation, I will just represent them using Greek symbols without specifying their potentially more complex natures.

Magnetic permeability (μ) reflects the degree to which matter concentrates or disperses an applied magnetic field. It is nearly synonymous with an already familiar concept, magnetic susceptibility (χ), connected by the relation μ = 1 + χ.

Permittivity (ε) is an electric property that serves as the homologue of magnetic permeability. It reflects the degree to which matter concentrates or disperses and applied electrical field. Higher permittivity means the material becomes more polarized when placed in an electric field. Permittivity is often used synonymously with dielectric constant, an older term that has fallen out of use.

Conductivity (σ) reflects the ability of a material to carry electrical current. Conductivity is inversely proportional to electrical resistance.

For weakly conductive dielectric materials such as those in the human body, the internal RF field is perturbed by a conductive current flux (J_C) and displacement current flux (J_D) that can be described by Ampère’s Law with Maxwell’s correction:

∇ Χ B = μJ_C + μJ_D = μσE + iωεE

where i² = −1 is the complex imaginary unit that introduces a 90° phase shift between the conductive and displacement currents. The ratio between the magnitudes of conductive and displacement currents is given by

J_C /J_D = σ / ω ε

In human tissues at RF-frequencies used in MRI J_C and J_D are of the same order of magnitude. As frequency increases the dielectric term (J_D) becomes more important, but even at 7.0T (300 MHz) the conductive/displacement current ratios for fat, gray matter, muscle, and CSF are approximately 0.4, 0.6, 0.7 and 1.7 respectively. High dielectric materials (such as those used in dielectric pads) may have ratios on the order of only 0.01, meaning the conductive current can be ignored.

---

References
      Collins CM, Liu W, Schreiber, et al. Central brightening due to constructive interference with, without, and despite dielectric resonance. J Magn Reson Imaging 2005; 21:192-6.
     Gabriel C, Gabriel S, Corhout E. The dielectric properties of biological tissues: I. Literature survey. Phys Med Biol 1996;41:2231-2249.    
     Webb AG, Collins CM. Parallel transmit and receive technology in high-field magnetic resonance neuroimaging (pdf). Int J Imaging Syst Technol 2010; 20:2–13.
     

---

Related Questions
     How do you reduce dielectric artifacts? How good are dielectric pads at solving this problem?  

---

←  Previous Question

Next Question  →

↑ Complete List of Questions ↑