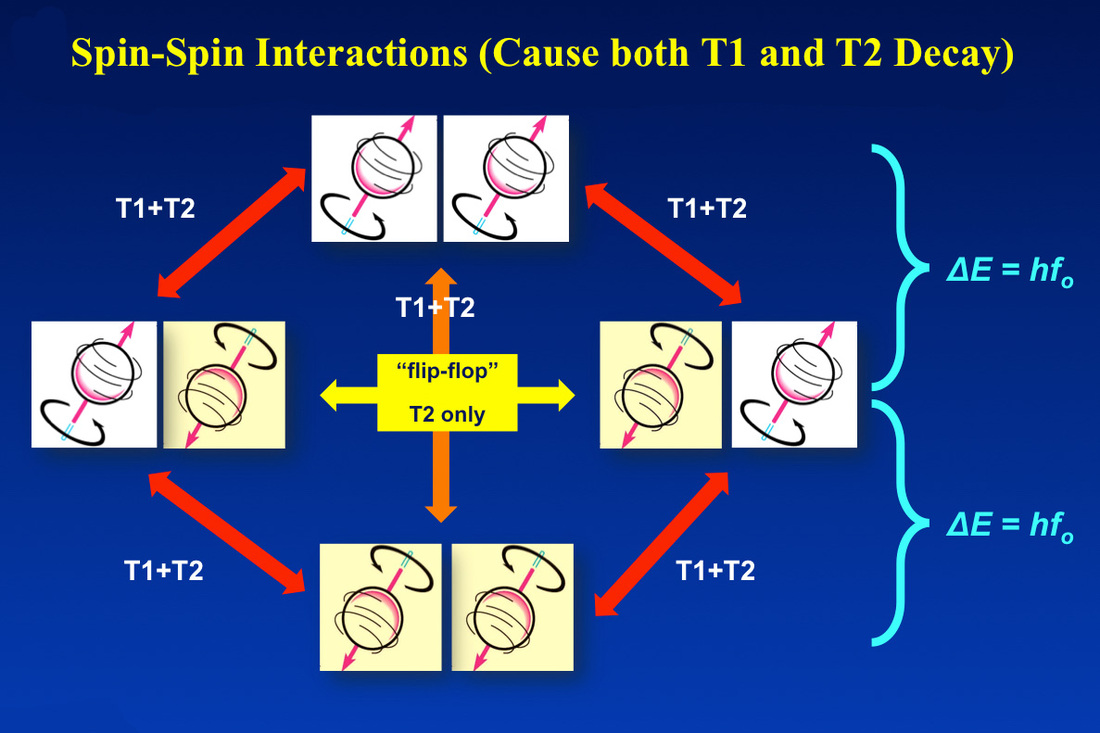
Consider the system of two spins shown below, which might be the two hydrogen protons on a water molecule (HOH). Depending on the initial orientations of the spins, several different outcomes may result. Most of these outcomes result in energy exchange and hence both T1 and T2 relaxation; other outcomes do not result in a net change in energy and T2 relaxation only.
In the diagram right I have shown two spins (nuclei/protons) in pure "spin-up" or "spin-down" states separated by energy quanta (ΔΕ = hfo). This has been done for simplicity/clarity only. As stated many times elsewhere on this site, spins are not restricted to these absolute orientations, but by doing so here the reasoning will hopefully be made easier to follow. |
An interesting interaction is seen in the middle of the diagram below, where an initially {up-down} pair of spins interacts resulting where both flip resulting in a final {down-up} state for the system. This is known as a "flip-flop". Although one spin has gained energy and the other lost energy, no net change in total system energy has occurred and hence no T1 relaxation. However, the interaction has randomly altered the angular momentum of both spins, so they no longer have any constant phase relationship to each other or to other spins in the sample. Hence, T2 relaxation alone has taken place.
A spin-spin interaction where there is a simultaneous state change of both spins (either of the double transition or flip-flop variety) is called cross-relaxation.
Advanced Discussion (show/hide)»
Although the simplified discussion above presents the two spins as acting independently, the true quantum mechanical analysis treats both spins together as a single wavefunction with four eigenstates |up-up>, |up-down>, |down-up>, and |down-down>. Just as single spins do not typically reside only in their eigenstates, neither does the double-spin system. Both the single and double-spin systems exist in superposition states (which are linear combinations of their eigenstates).
The double transition {up-up} ↔ {down-down} is accompanied by a total change in system energy of ħω + ħω = 2ħω = ħ(2ω). This can be considered an energy exchange occurring at twice the Larmor frequency and is consistent with the J(2ω) term appearing in the Solomon-Bloembergen equations. This phenomenon is a result of the dipole-dipole interaction and can be thought of as a sort of molecular Doppler effect. This is an internal/relative phenomenon and one would not see an absorption of energy or change in states by irradiating the the system with RF at frequency 2ω.
Levitt MH. Spin Dynamics. Basics of Nuclear Magnetic Resonance (2nd ed). Wiley, Chichester, 2012, pp 369-408.