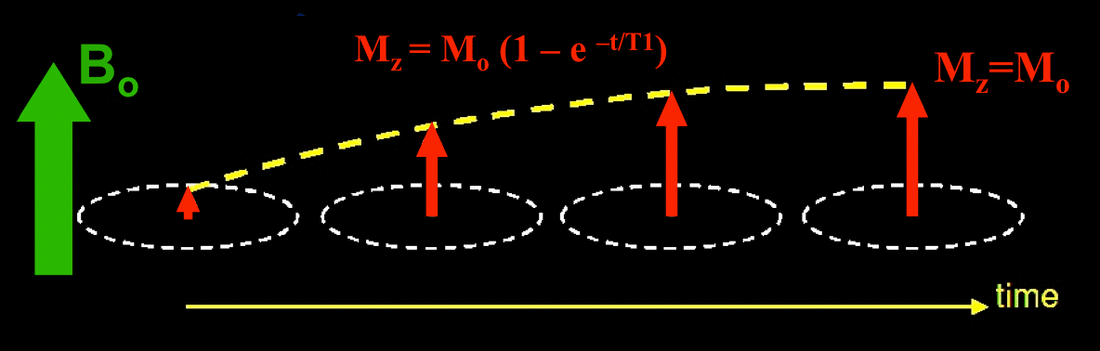
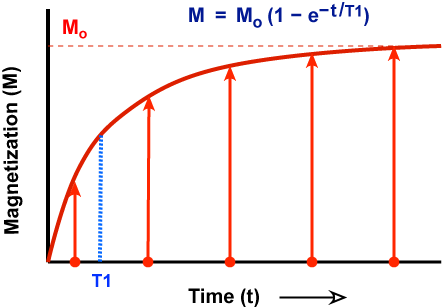
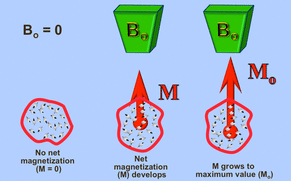
T1 Relaxation: Definition
What is T1 relaxation?
|
|
T1 relaxation is the process by which the net magnetization (M) grows/returns to its initial maximum value (Mo) parallel to Bo. Synonyms for T1 relaxation include longitudinal relaxation, thermal relaxation and spin-lattice relaxation. The meanings and implications of these synonyms will become apparent shortly.
T1 relaxation is the process by which the net magnetiztion (M) returns to its initial maximum value (Mo).
|
In his landmark 1946 paper describing "nuclear induction" (today called NMR), Felix Bloch modeled this process as a simple exponential with T1 as a first-order time constant. Graphically, therefore, T1 can be viewed as the time required for the z-component of M to reach (1 − 1/e) or about 63% of its maximum value (Mo). In biological materials, T1 values ranging from a few tenths of a second to several seconds are typically found.
|
Longitudinal relaxation is modeled as exponential growth curve with time constant T1. M reaches 63% of its maximum value (Mo) at t = T1 and is very close to maximal at t = 5 x T1.
|
The growth of M toward Bo is accompanied by reduction in energy within the spin system.
|
As the longitudinal component of M (Mz) grows toward Mo, the energy of the spin system decreases. Why? Because statistically more spins are "favoring" the lower energy (spin-up, parallel) orientation. (Remember, these spins don't actually reside in pure "spin-up" states, it is just that the expected value of their aggregate angular momentum comes to lie increasingly in that direction).
|
Energy must therefore leave the spin system for T1 relaxation to occur. This energy loss is unrecoverable and represents the transfer of heat; hence the origin of the T1 synonym "thermal relaxation". This energy must be transferred somewhere, and that "somewhere" is into nearby nuclei, atoms, and molecules through collisions, rotations, or electromagnetic interactions. At the most basic level, therefore, T1-relaxation is simply an energy flow between spins and their external environment. The amount of energy transferred from the nuclei is very small compared to normal molecular kinetic energies, so it is quickly dispersed and goes largely unnoticed at body temperatures.
In the early days of NMR studies in solids, this external environment was literally a crystalline lattice of atoms, giving origin to the T1 synonym "spin-lattice relaxation". Because biological NMR and MRI deals principally with liquids and gels rather than crystalline solids, I prefer to avoid the word "lattice" and call the process either longitudinal or T1-relaxation.
In the early days of NMR studies in solids, this external environment was literally a crystalline lattice of atoms, giving origin to the T1 synonym "spin-lattice relaxation". Because biological NMR and MRI deals principally with liquids and gels rather than crystalline solids, I prefer to avoid the word "lattice" and call the process either longitudinal or T1-relaxation.
As described in a previous Q&A, spontaneous emission of energy is extremely unlikely in the NMR range of frequencies. All energy emission in NMR must be stimulated through encounter of the nucleus with another magnetic field fluctuating near the Larmor frequency. The source of the locally fluctuating field necessary to induce relaxation is typically another proton or electron on the same or a nearby molecule. Just like the B1 field that originally excited nuclei into resonance, the RF-fields causing T1-relaxation must fluctuate near the Larmor frequency in the transverse plane.
The major difference between the original B1 field and fluctuating fields responsible for T1-relaxation is that the B1 field affects all spins in the sample uniformly. In relaxation, the fields are local, random in magnitude, and affect only a few spins.
The major "take-home" points about T1-relaxation are listed below.
The major difference between the original B1 field and fluctuating fields responsible for T1-relaxation is that the B1 field affects all spins in the sample uniformly. In relaxation, the fields are local, random in magnitude, and affect only a few spins.
The major "take-home" points about T1-relaxation are listed below.
T1 Relaxation Summary |
References
Bloch F. Nuclear induction (pdf). Phys Rev 1946; 70:460-474,1946. (This is the original paper in which Bloch derives his famous equations. Everyone serious about NMR should at least look over this paper -- it is very readable, even by those with little math or physics background -- many more words and explanations than equations.)
Bloch F. Nuclear induction (pdf). Phys Rev 1946; 70:460-474,1946. (This is the original paper in which Bloch derives his famous equations. Everyone serious about NMR should at least look over this paper -- it is very readable, even by those with little math or physics background -- many more words and explanations than equations.)
Spin-lattice relaxation. Wikipedia, The Free Encyclopedia.
Goldman M. Formal theory of spin-lattice relaxation (pdf). J Magn Reson 2001; 149:160-187. (Heavy paper for advanced physicists only, but this has everything in it).
Related Questions
Does the net magnetization (M) just instantly appear?
When a group of spins is driven into higher energy levels by the action of an RF field, why don't these spins immediately release the absorbed energy and drop back to their original lower energy states?
What is T2 relaxation?
What are the Bloch equations?
Does the net magnetization (M) just instantly appear?
When a group of spins is driven into higher energy levels by the action of an RF field, why don't these spins immediately release the absorbed energy and drop back to their original lower energy states?
What is T2 relaxation?
What are the Bloch equations?