Convolution

What does the term convolution mean?  

Have you ever used an app to remove red eye from a photo, sharpen a blurry picture, or change image contrast?  If so, then you have already used a convolution filter without knowing it!

In pure mathematical terms, a convolution represents the blending of two functions, f(x) and g(x), as one slides over the other. For each tiny sliding displacement (dx), the corresponding points of the first function f(x) and the mirror image of the second function g(t−x) are multiplied together then added. The result is the convolution of the two functions, represented by the expression [f *g](t).  

Cross-correlation ("Convolution") of two functions, f and g.
(from Wolfram MathWorld)

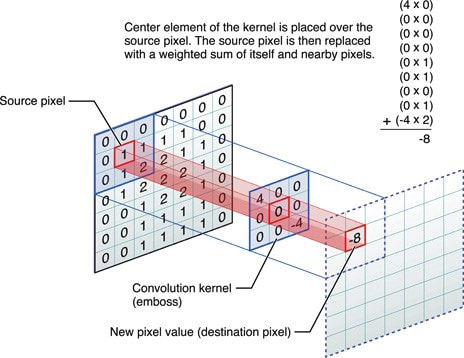
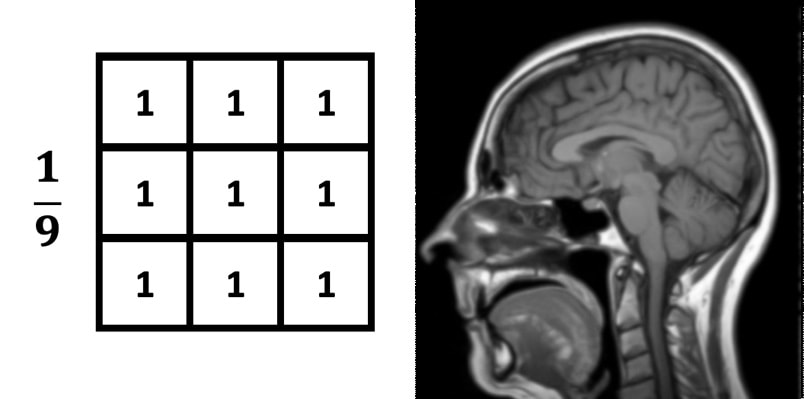
In image processing, convolution is performed by sliding a small array of numbers, typically a matrix of size [3x3] or [5x5], sequentially over different portions of the picture. This convolution matrix is also known as a convolution filter or kernel. For each position of the convolution matrix, the corresponding pixel values are multiplied and added together to replace the original center pixel.  In this way the values of the neighboring pixels are blended together with that of the central pixel to created a convolved feature matrix. The relative values of the matrix elements determine how that blending will affect the transformed image.

Identity Kernel: Just the starting image itself.

Sharpen Kernel:: Differences emphasized with its adjacent pixel values.

Left-to-right Sobel Kernel:. Used to accentuate differences between pixels along the horizontal axis

Box Blur Kernel: Each pixel is averaged equally with its 8 neighbors.

Outline ("Edge") Kernel: Highlights neighboring pixels with large differences of intensity.

Superior-to-inferior Sobel Kernel: Used to accentuate differences between pixels along the vertical axis.

These simple examples utilize 2D (planar filters), which are appropriate for black & white images such as those generated by magnitude-reconstructed MR.  Color images are commonly split into three channels (Red/Blue/Green) requiring 3D convolutional kernels. Similarly, more complex MR images (containing phase or velocity information, for example) may require higher dimensional filters.

Advanced Discussion (show/hide)»

In a strict mathematical sense, the process described as "convolution" in CNNs is technically a cross-correlation. In a true convolution, the function g is reversed/flipped horizontally before sliding it over function f. But here were are just sliding g over f without reversal, or performing a "sliding dot product" between two matrices. However, this incorrect nomenclature is not a big deal (to anyone except we mathematicians) because during the optimization of the CNN the filter weights are adjusted and don't necessarily have to be flipped at the beginning. Moreover the term "convolution" is so ingrained in the literature that it is impossible to change at this point in time, so we'll just live with the imprecise definition.

Some additional definitions are needed for completeness:

Kernel Size. This refers to the size of the sliding matrix that passes over the image. Usually the size is [3x3], [5x5], or [7x7]. Smaller kernel sizes provide better resolution of smaller features in the image and are generally preferred for MRI/radiology processing. The compromise is increased computational load from the many smaller convolutions produced at each step.

Padding. When the chosen kernel is near the edges and corners of the image, a part of the kernel will extend outside the image where there is no cell value to multiply. Although these empty values may simply be ignored, the more common method is to create extra pixels near the edges. This may be accomplished by one of several methods:

• Set a constant value for these pixels. If zero is chosen this is called “zero padding”.
• Duplicate the edge pixels
• Reflect edges (like a mirror effect)
• Wrap the image around (copying pixels from the other end)

Stride. Stride refers to the number of pixels the kernel moves between each convolution. Generally a stride = 1 is used, meaning that the sliding box moves one unit over at each step. This is what is pictured in the illustration above. A stride = 2 would mean the box would slide over 2 pixels at each step. The same resolution/complexity/computing time compromises for kernel size apply here.

---

References
     Amidi A, Amidi S. VIP Cheatsheet for CS 230 - Deep Learning: Convolutional Neural Networks. Stanford University; 2019:1-5.  [Downloaded from this Link 6-22-22] 
     Ganesh P.  Types of convolution kernels: simplified. Toward Data Science. 2019:1-12. [Downloaded from this link 2-9-22]
     Weisstein, Eric W. "Convolution." From MathWorld--A Wolfram Web Resource (downloaded from  https://mathworld.wolfram.com/Convolution.html 6 Feb 2022)

---

Related Questions
     I still don't understand how machines learn. How do they "reprogram" themselves?

---

←  Previous Question

Next Question  →

↑ Complete List of Questions ↑