Upsampling

What is upsampling? Why might one want to perform this action on a previously convoluted data set?

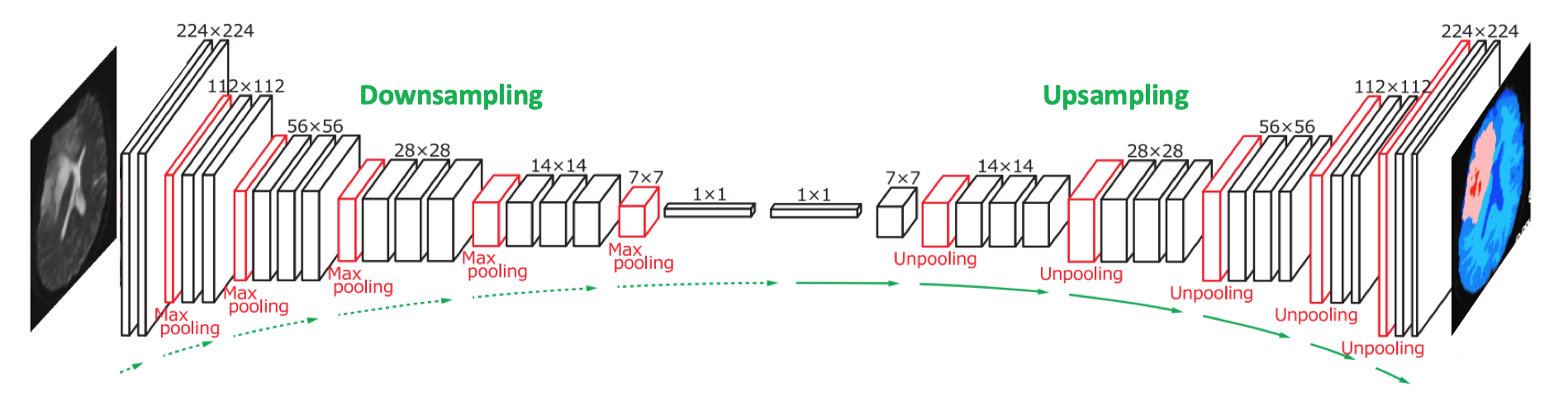
The initial convolutional and pooling layers of a CNN progressively reduce the spatial dimensions (width and height) of the input and intermediate feature maps, a process known as encoding or downsampling. This produces a compressed representation of the input image that can be efficiently processed, allowing the network to extract key structural features and relationships within the input.

For many image processing applications (such as segmentation, co-registration, artifact removal, and image enhancement) it may be desirable to reverse the process, gradually restoring the spatial dimensions of the feature maps while reducing the number of channels or features. This process is known as upsampling (also called decoding, unpooling, or upscaling). Sequential downsampling and upsampling is the basis of encoder-decoder networks, one of the more commonly used image-processing AI architectures. Because of their shape, such configurations are also called U-networks.

Encoder-decoder network, consisting of a convolution/pooling portion that reduces image dimensions (downsampling) followed by an upsampling portion which returns image dimensions to its original size (here with a tumor segmentation overlay).

Several methods exist for the upsampling portion of th

Interpolation Methods for Upsampling

Nearest Neighbor: This method involves duplicating the existing pixels or samples to create new ones. It is the simplest and fastest method but may result in a blocky or pixelated appearance.
Bed of NailsTechnique: Unlike Nearest Neighbor, the Bed-of-Nails only inputs one of the input elements in each region, setting the rest to zero.
Max Unpooling: This is similar to the Bed-of-Nails but places elements in the larger matrix at locations from where they originally occurred. (This requires memory of their original locations).
Bilinear Interpolation: This method computes the value of new pixels by taking a weighted average of the nearest four pixels. It results in a smoother image than nearest neighbor interpolation but may introduce artifacts such as blurring and aliasing.
Bicubic Interpolation: This method uses a more complex interpolation algorithm that takes into account 16 neighboring pixels to compute the value of new pixels. It results in a higher-quality image than bilinear interpolation but requires more computational resources.
Lanczos Interpolation: This method uses a weighted average of a larger number of neighboring pixels to compute the value of new pixels. It produces sharp and detailed images but requires a larger kernel size and more computational resources.

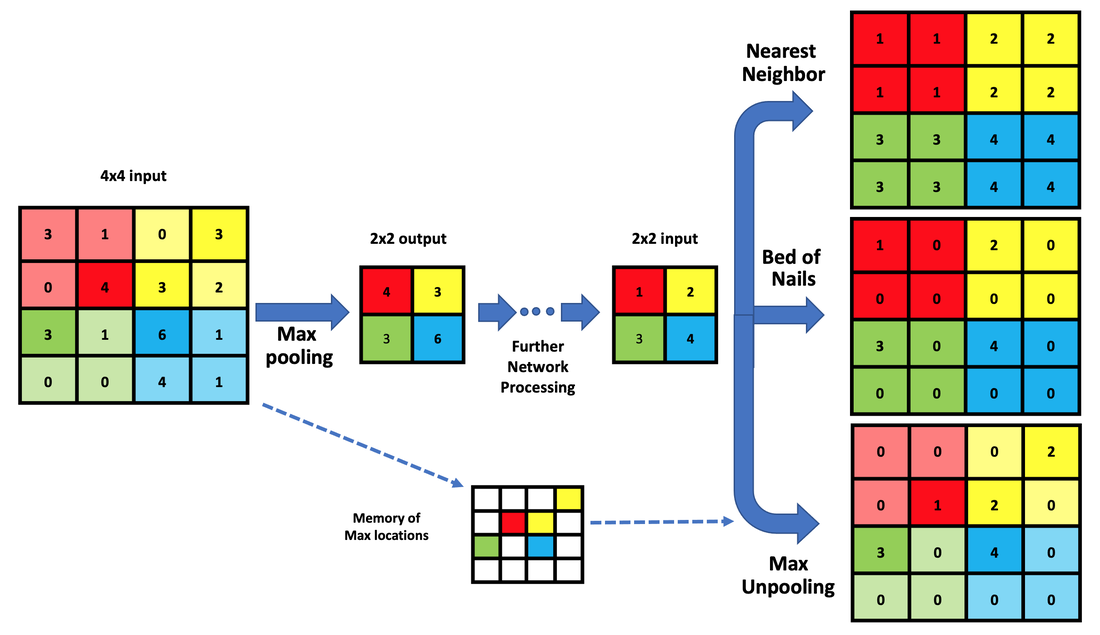
Three types of unpooling/upscaling to increase size of feature maps from 2x2 to 4x4. Nearest Neighbor Unpooling replicates each element of the 2x2 input into 4 identical adjacent locations in the 4x4 matrix. The Bed of Nails method only replicates one of the input elements in corresponding 2x2 regions, setting the rest to zero. Max Unpooling is similar to the Bed of Nails, but places elements in the larger matrix at locations from where they originally occurred.

Transposed Convolution

Transposed convolution, also called (backward) strided convolution, is one of the more common and sophisticated techniques for upsampling or enlarging feature maps. It involves applying a learned convolutional filter to the reduced size feature maps in a way that reverses the effects of the original convolution operation. This is a learnable method that can be optimized during training and is effective for generating high-quality images of larger size.

In "regular" convolution, a small kernel or filter is slid across the input signal or feature map, producing a set of output features or channels. The output feature map is typically smaller than the input, due to the kernel size and stride.

In transposed convolution, the process is reversed. Instead of applying a kernel to a local region of the input, a kernel is applied to each location of the output feature map, with a stride that determines the distance between successive kernel positions. Each kernel output is then added to the corresponding location in the output feature map. The transposed convolution broadcasts input elements via the kernel, thereby producing an output that is larger than the input. A simple example is shown below.

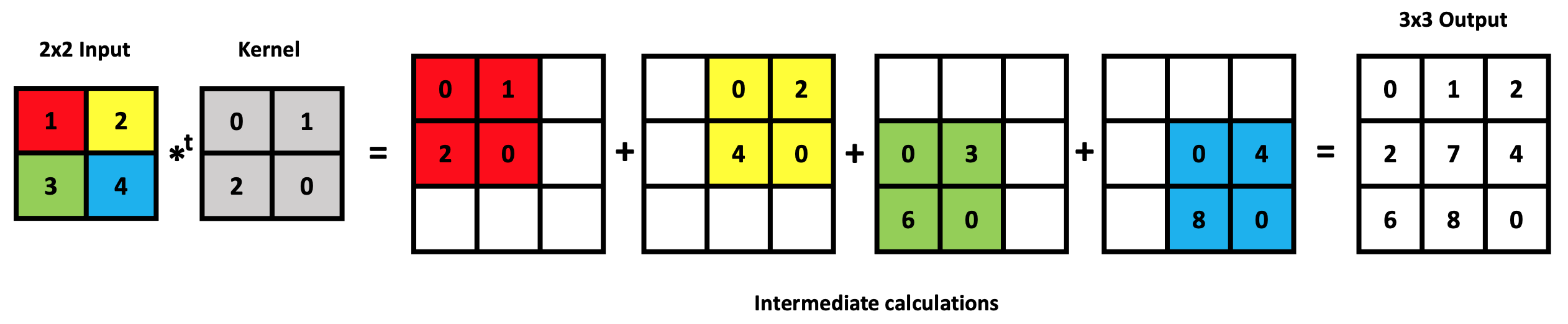
Transposed Convolution of 2x2 input with a 2x2 kernel to produce a 3x3 output. At each step, a single element (e.g., red) of the input matrix multiplies all 4 kernel elements, with the result placed in an intermediate 3x3 matrix at a location corresponding to position of the red input element. The process is repeated for the three other input elements. The four intermediate matrices are added together to create the final 3x3 output.

Advanced Discussion (show/hide)»

References
Dumoulin V, Visin F. (2016). A guide to convolution arithmetic for deep learning. arXiv preprint arXiv:1603.07285.
Maier A, Syben C, Lasser T, Riess C. A gentle introduction to deep learning in medical image processing. Z Med Pay 2019; 29:86-101. [DOI LINK]
Noh H, Hong S, Han. Learning deconvolution network for semantic segmentation. Proceedings of ICCV, 2015. [arXiv LINK]
Siddique N, Paheding S, Elkin CP, Devabhaktuni V. U-Net and its variants for medical image segmentation: a review of theory and applications. IEEE Access 2021:82031-82057. [DOI LINK]

← Previous Question

Next Question →

↑ Complete List of Questions ↑