Precession
All the NMR books all show protons precessing like little tops or gyroscopes within the magnetic field. I don't really understand why this type of motion should occur. Can you explain?
|
|
|
|
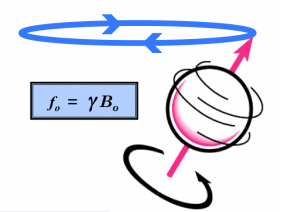
Nuclei precess around the magnetic field for essentially the same reasons that tops or gyroscopes precess around a gravitational field:
1) Both gyroscopes and nuclei possess angular momentum. For the gyroscope, angular momentum results from a flywheel rotating about its axis. For the nucleus, angular momentum results from an intrinsic quantum property (spin).
2) Momentum is also sometimes called inertia. Objects possessing momentum have a tendency to maintain their motion unless acted upon by an external force. For example, a speeding truck has a great deal of (linear) momentum and cannot easily be induced to change its speed or direction. Angular momentum behaves similarly, conferring on the nucleus or gyroscope a strong resistance to changing its orientation or direction of rotation.
3) Static gravitational and magnetic fields create a torque or "twisting force" acting perpendicular to both the field and the direction of the angular momentum. The gyroscope or nucleus does not "tip over" but is instead deflected into a circular path perpendicular to the field.
4) The resultant circular motion is called precession. Precession occurs at a specific frequency denoted either by ωo (called the angular frequency, measured in radians/sec) or fo (called the cyclic frequency, measured in cycles/sec or Hertz [Hz]). Since 2π radians = 360° = 1 cycle (revolution), angular and cyclic frequencies can easily be converted by the equation: ωo = 2 π fo
5) The precession frequency of a gyroscope is a function of the mass and shape of the wheel, the speed of wheel rotation, and the strength of the gravitational field. The precession frequency of a nucleus is proportional to the strength of the magnetic field (Bo) and the gyromagnetic ratio (γ), a particle-specific constant incorporating size, mass, and spin. This is embodied in the famous Larmor relationship, given by the equation: fo = γ Bo
1) Both gyroscopes and nuclei possess angular momentum. For the gyroscope, angular momentum results from a flywheel rotating about its axis. For the nucleus, angular momentum results from an intrinsic quantum property (spin).
2) Momentum is also sometimes called inertia. Objects possessing momentum have a tendency to maintain their motion unless acted upon by an external force. For example, a speeding truck has a great deal of (linear) momentum and cannot easily be induced to change its speed or direction. Angular momentum behaves similarly, conferring on the nucleus or gyroscope a strong resistance to changing its orientation or direction of rotation.
3) Static gravitational and magnetic fields create a torque or "twisting force" acting perpendicular to both the field and the direction of the angular momentum. The gyroscope or nucleus does not "tip over" but is instead deflected into a circular path perpendicular to the field.
4) The resultant circular motion is called precession. Precession occurs at a specific frequency denoted either by ωo (called the angular frequency, measured in radians/sec) or fo (called the cyclic frequency, measured in cycles/sec or Hertz [Hz]). Since 2π radians = 360° = 1 cycle (revolution), angular and cyclic frequencies can easily be converted by the equation: ωo = 2 π fo
5) The precession frequency of a gyroscope is a function of the mass and shape of the wheel, the speed of wheel rotation, and the strength of the gravitational field. The precession frequency of a nucleus is proportional to the strength of the magnetic field (Bo) and the gyromagnetic ratio (γ), a particle-specific constant incorporating size, mass, and spin. This is embodied in the famous Larmor relationship, given by the equation: fo = γ Bo
|
|
As a further introduction to the concept of angular momentum and precession, I strongly suggest viewing the YouTube video of the late Sir Paul Callaghan, a famed New Zealand NMR researcher.
Before he died, Dr. Callahan posted an excellent set of 10 short videos on the internet demonstrating the basic concepts of NMR and MRI as his lasting legacy. I have attached these to various Q&A's throughout this web site. His full set of videos can be found here. |
References
Butikov E. Precession and nutation of a gyroscope. Also from this link (accessed 2016).
Butikov E. Precession and nutation of a gyroscope. Also from this link (accessed 2016).
Related Questions
What is spin?
Why does the RF-field have to be applied exactly at the Larmor frequency for resonance to occur?
What is spin?
Why does the RF-field have to be applied exactly at the Larmor frequency for resonance to occur?