Zero-Interpolation Filling 

A option called ZIP is available for some sequences. Is this a type of file compression?  

Processing of MRI data is usually performed in an array processor using the Fast Fourier Transform (FFT) algorithm. These computational requirements generally require the input data to be in a matrix whose dimensions are a power of 2, such as 128x128, 256x256, or 512x512. If the acquired k-space data does not complete this matrix, it is customary to fill in the missing cells with zeroes, a technique called zero padding, zero filling, or zero-interpolation filling (ZIP). 

ZIP in MRI has nothing to do with the *.zip technique of file compression. And nothing to do with postal codes either!

Zero-filling is routinely used to expand the image matrix size in the phase-encoded direction. For 2D imaging this increase in matrix size is "within-plane" (e.g., from 256 to 512 pixels). For 3D imaging ZIP can be used "through-plane" to increase apparent resolution in the slab-select direction (e.g., from 64 to 128 slices). The gains occur for the first doubling of matrix size; thereafter, no benefit is realized.

Although zero-filling does not add any information to the input raw data, it can nevertheless improve the apparent spatial resolution of the image due to reduced partial volume artifacts. Zero filling acts as method to interpolate the signals from neighboring voxels, giving the image a smoother and less "pixel-ly" appearance.

Examples of cranial MRAs without and with zero-interpolation (ZIP) filling.
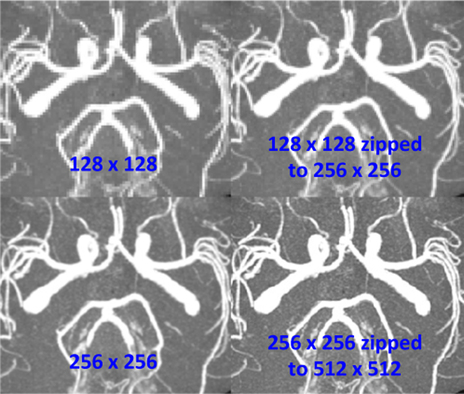
On left, images acquired with full data in 128x128 and 256x256 matrices.
On right, ZIP filling has been performed, increasing matrix size to 256x256 and 512x512 respectively.
Note improvement in image quality, especially for the 128x128 data set.

Advanced Discussion (show/hide)»

Why is zero-filling k-space similar to pixel-interpolation in image space? The underlying mathematics is somewhat difficult, and the interested reader is referred to the various references below (especially the Bartholdi-Ernst paper) as a place to start.

In brief, regardless of how large a matrix is chosen, it is always smaller than the theoretically infinite k-space representation of an object and must be truncated (cut short) at some point. Truncation is equivalent to multiplication of the k-space data by a "boxcar"/rectangle function. This, in turn is equivalent to convolution in image space with a SINC function (which is the Fourier transform of a rectangle function). Zero-filling produces additional SINC-interpolated pixels in the display matrix.

A fascinating result is that the initial doubling the number of data points through zero filling actually does add "fresh information" beyond simple interpolation. But how can extra zero's constitute "new" data? The reason they help is that the plain FFT does not extract all the information available in an FID. By doubling the number of points, the FFT becomes more efficient at extracting all "true" data. It's not so much that ZIP creates new information, but that the standard FFT is insufficient at digging out all that is available. Beyond the initial doubling, no advantage accrues, as the Fourier coefficients now become fully correlated with each other. Hence only one ZIP step is generally used in data processing.

As described above, in 2D imaging, ZIP is applied "in-plane". In 3D imaging, ZIP may be applied "in-plane", "through plane" or both. Vendors have different nomenclature for these two types of ZIP. GE Healthcare, for example, denotes in-plane ZIP as "ZIP 512" or "ZIP 1024" while referring to through-plane ZIP as "ZIP x 2" or "ZIP x 4".

---

References
     Bartholdi E, Ernst RR. Fourier spectroscopy and the causality principle. J Magn Reson 1973; 11:9-19.   
     Bernstein MA, Fain SB, Riederer SJ. Effect of windowing and zero-filled reconstruction of MRI data on spatial resolution and acquisition strategy. J Magn Reson Imaging 2001;14:270-280.
     Du YP, Parker DL, Davis WL, Cao G. Reduction of partial volume artifacts with zero-filled interpolation in three dimensional MR angiography. J Magn Reson Imaging 1994; 4:733-741     
     Ebel A, Dreher W, Leibfritz D. Effects of zero-filling and apodization on spectral integrals in discrete Fourier-transform spectroscopy of noisy data. J Magn Reson 2006;182:330-338.
     Lindon JC, Ferrige AG. Digitisation and data processing in Fourier transform NMR. Prog NMR Spect 1980; 14:27-66. (Although adding zero interpolation filling beyond the first FT step does not provide independent information, it can occasionally be useful in spectroscopy to better define a line or peak position more precisely)
     Zhu X, Tomanek B, Sharp J. A pixel is an artifact: on the necessity of zero-filling in Fourier imaging. Concepts Magn Reson 2013; 42A:32-44. (Interesting paper showing how constraining images into pixels attenuates high spatial frequencies and introduces high frequency artifactual structure.)

---

Related Questions
     Why is k-space drawn as a grid? What do the axes in k-space mean?  

---

←  Previous Question

Next Question  →

↑ Complete List of Questions ↑