Off-resonance effects
What happens if the B1 field is applied "off resonance" (i.e., not exactly at the Larmor frequency)?
|
|
In previous Q&A's I was careful to say that the B1 field needed to be applied at a frequency near the Larmor frequency. However, no B1 field is perfect and hence even when exactly the Larmor frequency is desired there will be portions of the image or sample that may not experience exactly this frequency. Additionally there are a number of interesting MR techniques in which the B1 frequency is purposely offset from resonance or swept through frequencies on either side of the Larmor frequency. These situations become more understandable by using the rotating frame analysis in the previous question. If you have not yet reviewed this Q&A I suggest you do so now before launching into the discussion below.
|
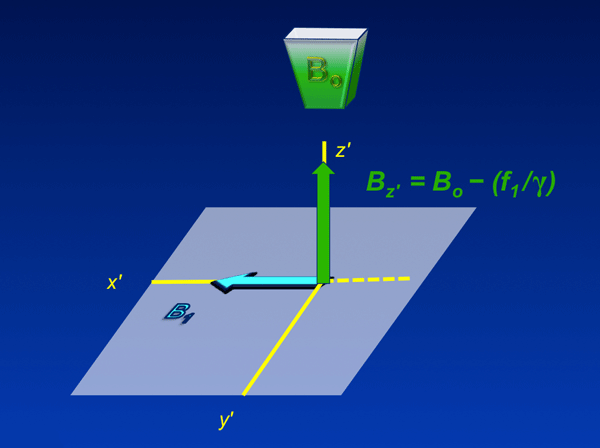
The diagram to the left is a more general form of the rotating frame described previously that allows us to consider what happens when B1 is applied at frequency f1 that may not be exactly the Larmor frequency fo = γ Bo.
The rotating frame is locked into sync with the B1 field at frequency f1. If f1 ≠ fo then the Bo field does not completely disappear in the rotating frame. Instead there is some residual longitudinal magnetization given by Bz' = (fo − f1) / γ = Bo − (f1/γ)
You can see that when f1 = fo = γ Bo, Bz' = 0, which is what we expect.
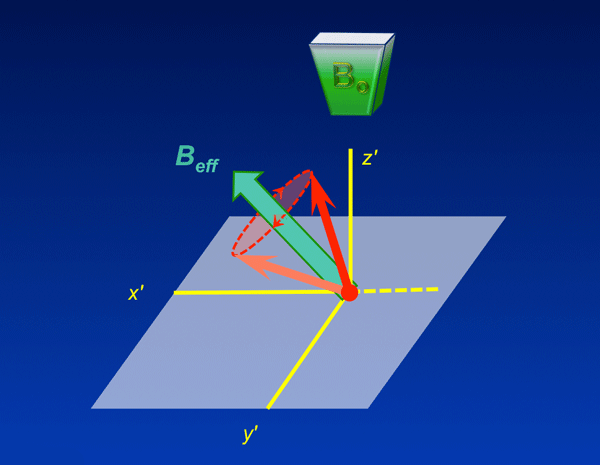
Together B1 and Bz' vectorially add together to produce an effective field (Beff) in the rotating frame. The magnitude and orientation of Beff can be determined by the Pythagorean Theorem and simple trigonometry. |
|
When B1 is applied off-resonance (i.e., not exactly at the Larmor frequency) the trajectory of M is more complex. Instead of precessing around B1, M now precesses in a cone around Beff at frequency feff = γ Beff.
At this point we will not go into any more detail about the rotating frame and off-resonance effects, but we will return to them in later Q&A's where concepts like adiabatic following and spin locking will be discussed. |
References
Keeler J. The vector model. From The Keeler Group, Lectures by James Keeler, 2004 (http://www-keeler.ch.cam.ac.uk/lectures/)
Rabi II, Ramsey NF, Schwinger J. Use of rotating coordinates in magnetic resonance problems. Rev Mod Phys 1954; 26(2):167-171.
Redfield AG. Nuclear magnetic resonance saturation and rotary saturation in solids. Phys Rev 1955; 98:1787-1809. (This paper, considered one of the most important in early NMR, showed that the Bloch equations, though accurate in liquids, violated the Second Law of Thermodynamics in solids. Redfield expands upon the rotating frame concept here leading to a better understanding of spin ordering, spin locking, and adiabatic phenomena.)
Ulmer JL, Mathews VP, Hamilton CA, Elster AD, Moran PR. Magnetization transfer or spin-lock? An investigation of off-resonance saturation pulse imaging with varying frequency offsets. AJNR Am J Neuroradiol 1996; 17:805-819. (See Appendix for a simplified discussion of rotating frame and spin-locking.)
Keeler J. The vector model. From The Keeler Group, Lectures by James Keeler, 2004 (http://www-keeler.ch.cam.ac.uk/lectures/)
Rabi II, Ramsey NF, Schwinger J. Use of rotating coordinates in magnetic resonance problems. Rev Mod Phys 1954; 26(2):167-171.
Redfield AG. Nuclear magnetic resonance saturation and rotary saturation in solids. Phys Rev 1955; 98:1787-1809. (This paper, considered one of the most important in early NMR, showed that the Bloch equations, though accurate in liquids, violated the Second Law of Thermodynamics in solids. Redfield expands upon the rotating frame concept here leading to a better understanding of spin ordering, spin locking, and adiabatic phenomena.)
Ulmer JL, Mathews VP, Hamilton CA, Elster AD, Moran PR. Magnetization transfer or spin-lock? An investigation of off-resonance saturation pulse imaging with varying frequency offsets. AJNR Am J Neuroradiol 1996; 17:805-819. (See Appendix for a simplified discussion of rotating frame and spin-locking.)
Related Questions
What is the rotating frame of reference?
What is the rotating frame of reference?