Flow and MRA

Can you explain even-echo rephasing? 

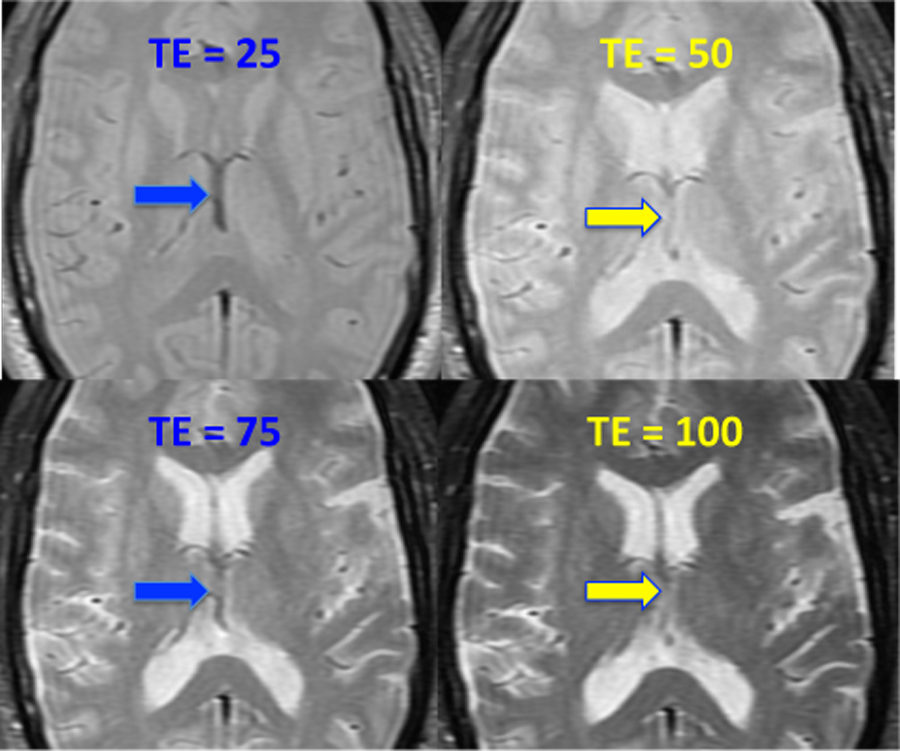
Even-echo rephasing is a flow phenomenon that is observed in SE images in which multiple evenly spaced echoes (e.g., 25/50/75/100) have been acquired.  For blood flowing at constant velocity in such an environment, phase dispersion is lower on the even-numbered echoes (i.e., 50/100) than on the odd echoes (i.e., 25/75).  The absolute increase in flow signal on the second and fourth echoes is called even-echo rephasing;  the loss in signal on the first and third echoes is called odd-echo dephasing.  

Odd-echo dephasing (TE=25 and 75) and even-echo rephasing (TE=50 and 100) noted in the internal cerebral veins (arrows). The veins' signals are increased on the even numbered echoes.

This modulation of signal by echo number is caused by the frequency-encoding gradient.  Hence this phenomenon is typically seen in vessels flowing within an imaging plane and having some component of flow in the frequency-encode direction. The internal cerebral veins pictured above are running exactly in the frequency-encode direction, explaining why the phenomenon is so prominent in these vessels.

Even-echo rephasing and odd-echo dephasing derive from the fact explained in a prior Q&A that steady flow in a constant gradient results in a phase shift that is quadratic in time. When these phase shifts are inverted by 180°-pulses, the quadratic phase dispersions cancel out at alternate echoes. A more complete mathematical explanation for why even-echo rephasing and odd-echo dephasing occur can be found in the Advanced Discussion below, or in the classic reference by Waluch and Bradley.

Even-echo rephasing is mainly of historic interest, since simple multi-echo spin echo imaging of the type illustrated above is seldom performed any more, having been replaced by fast (turbo) spin echo methods. However, FSE imaging does utilize multiple symmetric echoes, so both even-echo rephasing and odd-echo dephasing operate "behind the scenes" to modulate the final MR signal in flowing vessels observed on these sequences.

Advanced Discussion (show/hide)»

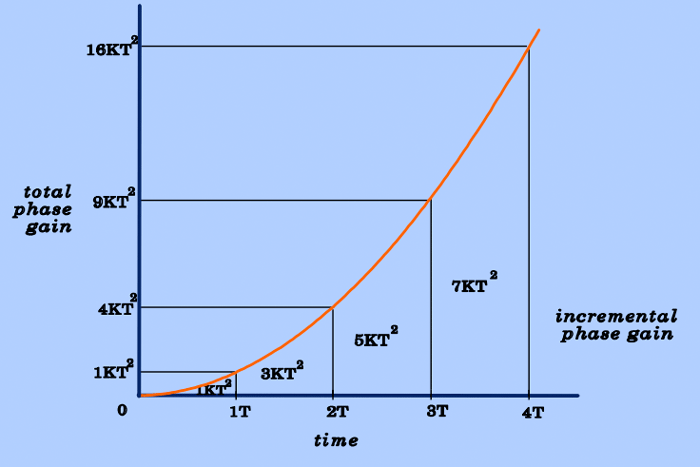
To explain why even-echo rephasing and odd-echo dephasing occur, it is necessary to make use of a fact developed in a prior Q&A that for constant velocity flow (v) through a constant gradient (G), total phase shift (Φ) increases quadratically with time (T).  In other words 

Φ =  KT² 

where K = ½ γ G v is a constant when velocity and readout gradient strength are also constant.  

This quadratic dependence of total phase gain upon time is shown in the figure below.  Note that after 1, 2, 3, and 4 gradient intervals each of duration T, the phase has increased quadratically to KT², 4KT², 9KT², and 16KT² respectively.  The incremental phase contributions of the 1st, 2nd, 3rd, and 4th gradient intervals are therefore  KT², 3KT², 5KT², and 7KT², respectively.

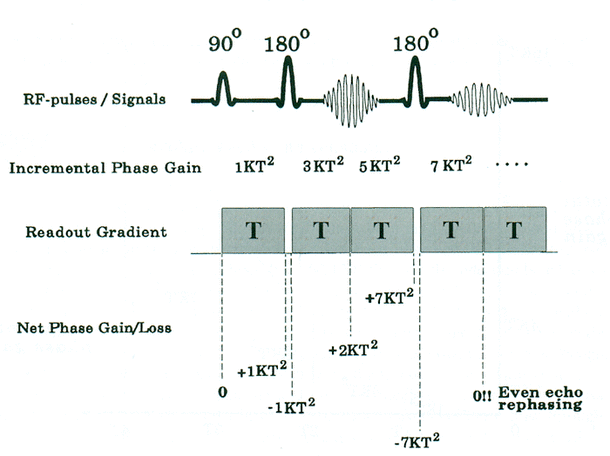
Using these calculated incremental phase contributions from each block of the gradient, we now can calculate what the phase should be at each point in a multiple spin echo protocol.  Let us first consider the action of the 180°-pulses, which invert the level of accumulated phase existing immediately before the pulse.  After block 1 but before the 180°-pulse, the total accumulated phase is  KT².  Immediately after the 180°-pulse the total phase has been inverted to −KT².  The next block adds 3KT² of phase, after which the total phase at the center of the first echo is 2KT² (i.e., −KT² + 3KT²).  Thus the first echo has an appreciable phase dispersion because of flow.  This is the origin of odd-echo dephasing.

Continuing, we see that the readout gradient for the first echo contains another block, which adds another 5KT² of phase.  After this block and immediately before the next 180°-pulse, the total phase has reached 2KT² + 5KT² = 7KT².  The 180°-pulse inverts this phase, so immediately after the 180° pulse the total phase is  −7KT².  To get to the center of the second echo, we must add the incremental phase contribution of the 4th block, which we have previously computed to be 7KT².  The total phase at the center of the second echo is therefore −7KT² + 7KT²− = 0!  In other words, moving spins have come back into phase at the center of the second echo.  This is the origin of even-echo rephasing.

Although this simplified analysis assumes that the gradient pulses are applied back-to-back, the same results can be demonstrated even when the gradients are spaced out, as they normally are on routine imaging.

---

References
       Waluch V, Bradley WG Jr.  NMR even echo rephasing in slow laminar flow.  J Comput Assist Tomogr 1984; 8:594-8.    

---

Related Questions
     What are spin-phase effects?  

---

←  Previous Question

Next Question  →

↑ Complete List of Questions ↑