How Magnetization Develops
Does the net magnetization (M) just instantly appear?
|
|
Development of net magnetization (M) when a sample is first placed in a magnetic field (Bo).
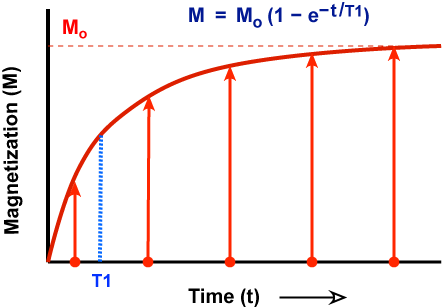
M grows as a simple exponential with time constant T1. T1 is also called the spin-lattice, thermal or longitudinal relaxation time. On the graph it corresponds to the time required for M to grow to (1 − 1/e) or about 63% of its final value (Mo). We will have much, much more to say about T1 in future Q&A's!
|
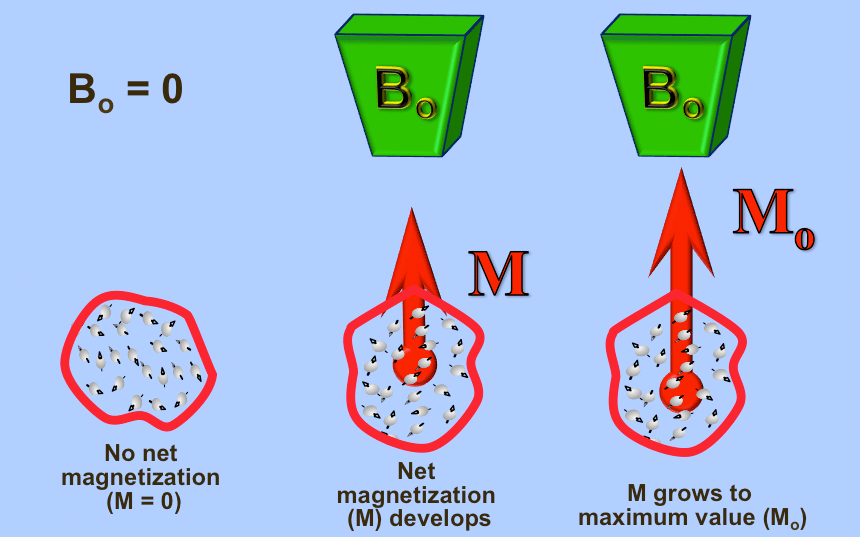
No. It may take up to several seconds for the net magnetization (M) to fully develop when an unmagnetized substance is first placed in an external magnetic field (Bo). It will grow until it reaches a final equilibrium value of Mo. 
Growth of longitudinal magnetization (M) with time after being placed in magnetic field is a simple exponential with time constant (T1).
|
Related Questions
If a system seeks to minimize its total energy level, why don't all the protons simply fall into the lower energy state?
What is net magnetization and how does it apply to NMR?
If a system seeks to minimize its total energy level, why don't all the protons simply fall into the lower energy state?
What is net magnetization and how does it apply to NMR?