Steady-State Magnetization
Wait a minute! If a partial flip angle pulse tips less magnetization into the transverse plane than a 90° pulse does, how can the signal be higher?
|
|
At first it seems paradoxical that reducing the flip angle (and hence the fraction of longitudinal magnetization deflected into the transverse plane) could ever produce a stronger signal than is produced by using 90°-pulses. Indeed, if only a single RF pulse were applied, then a 90°-flip angle would always be optimal. But an an MR imaging sequence involves the application of repetitive RF pulses, and for reasons described below, a series of 90°-pulses may not produce the highest signal.
Recall that before any RF-pulses are applied, the spin system reaches a state of thermal equilibrium with its environment. As described in a prior Q&A, the system develops a net longitudinal magnetization (Mz) whose initial maximum value is denoted Mo. The first RF-pulse rotates some (or all) of Mz into the transverse plane to generate a signal. The transverse component created is [Mo sin α] where α is the flip angle. When α = 90°, all of Mz is converted into transverse magnetization with maximal value Mo.
But we must now consider the effects of the second and subsequent RF-pulses applied after the first RF-pulse. The spacing of between successive RF-pulses is called the repetition time (TR).
Immediately after RF-excitation, the longitudinal magnetization (Mz) has been partially or completely obliterated, having been converted into transverse magnetization. During the TR interval, Mz will regrow in an exponential fashion with time constant T1. If TR is sufficiently long (the usual requirement is TR > 4-5x T1), Mz will have time to completely recover and be restored to its full initial magnetization Mo.
But what happens if TR is not long compared to T1? In this case the second and subsequent pulses occur before Mz has returned to its initial maximum value (Mo). After a few pulses a new steady-state longitudinal magnetization (Mss) will be established, where Mss < Mo. This phenomenon is called partial saturation, meaning that the spin system has not fully relaxed back to its equilibrium condition.
Recall that before any RF-pulses are applied, the spin system reaches a state of thermal equilibrium with its environment. As described in a prior Q&A, the system develops a net longitudinal magnetization (Mz) whose initial maximum value is denoted Mo. The first RF-pulse rotates some (or all) of Mz into the transverse plane to generate a signal. The transverse component created is [Mo sin α] where α is the flip angle. When α = 90°, all of Mz is converted into transverse magnetization with maximal value Mo.
But we must now consider the effects of the second and subsequent RF-pulses applied after the first RF-pulse. The spacing of between successive RF-pulses is called the repetition time (TR).
Immediately after RF-excitation, the longitudinal magnetization (Mz) has been partially or completely obliterated, having been converted into transverse magnetization. During the TR interval, Mz will regrow in an exponential fashion with time constant T1. If TR is sufficiently long (the usual requirement is TR > 4-5x T1), Mz will have time to completely recover and be restored to its full initial magnetization Mo.
But what happens if TR is not long compared to T1? In this case the second and subsequent pulses occur before Mz has returned to its initial maximum value (Mo). After a few pulses a new steady-state longitudinal magnetization (Mss) will be established, where Mss < Mo. This phenomenon is called partial saturation, meaning that the spin system has not fully relaxed back to its equilibrium condition.
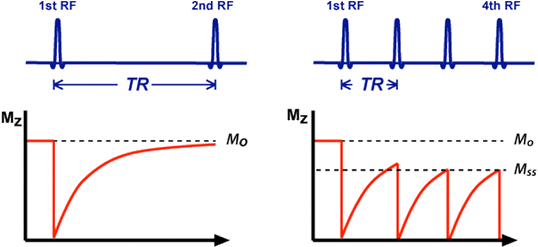
Partial saturation and development of steady-state magnetization (Mo)
[left] TR >> T1 so there is complete recovery of Mz back to Mo before the 2nd RF-pulse.
[right] TR is shorter and Mz does not fully recover before next RF-pulse is applied. After a few pulses a new steady-state longitudinal magnetization (Mss) is reached, with Mss < Mo. Note that in this second figure part we have assumed that TR>>T2, so that there is no build-up of transverse coherences from cycle to cycle.
[left] TR >> T1 so there is complete recovery of Mz back to Mo before the 2nd RF-pulse.
[right] TR is shorter and Mz does not fully recover before next RF-pulse is applied. After a few pulses a new steady-state longitudinal magnetization (Mss) is reached, with Mss < Mo. Note that in this second figure part we have assumed that TR>>T2, so that there is no build-up of transverse coherences from cycle to cycle.
With this concept of partial saturation and the development of steady-state longitudinal magnetization (Mss) in place, we can now see why a series of partial flip angle pulses may produce a higher overall signal than a series of 90°-pulses.
Each 90°-pulse tips 100% of Mz into the transverse plane, driving the steady-state magnetization (Mss) and MR signal to a low level.
Each low-flip angle pulse tips less of Mz into the transverse plane, leaving residual longitudinal magnetization for the next RF-pulse. The steady-state magnetization (Mss) and MR signal are therefore higher.
|
In summary, the amplitude of the MR signal represents a "balancing act" between two factors: (1) the value of the steady-state longitudinal magnetization (Mss) and (2) the fraction of Mz tipped into the transverse plane by each RF-pulse. Although 90°-pulses tip the largest fraction of magnetization into the transverse plane, they also reduce the magnitude of Mz, and overall MR signal is not necessarily maximized. Conversely, partial flip angle pulses tip a smaller fraction of magnetization into the transverse plane but reduce Mz less. Overall, therefore, a series of partial flip angle pulses may generate a stronger signal than is generated by a series of 90° pulses.
References
Haase A, Frahm J, Matthaei KD. FLASH imaging: rapid NMR imaging using low flip angle pulses. J Magn Reson 1986: 67: 258-266.
Haase A, Frahm J, Matthaei KD. FLASH imaging: rapid NMR imaging using low flip angle pulses. J Magn Reson 1986: 67: 258-266.
Related Questions
What is a partial flip angle pulse, and why would you want to use one?
What is a partial flip angle pulse, and why would you want to use one?