Tesla Defined

We have a 3.0 tesla MR scanner at our hospital.  I know this is a very strong magnet, but what exactly is a tesla?  

Definition of B

The simplified definition of tesla describes only the magnitude (B) of the field at a given point.  If the field is perfectly uniform, B is the same at all points within the field.  In general, however, the structure of the magnetic field is more complex, and B may have different values and directions of action at different points in space.  A magnetic field is therefore formally defined to be an array of vectors (denoted by the boldfaced letter B) whose magnitude B and direction at each point in space define how the field will act on a charge moving at that location.  

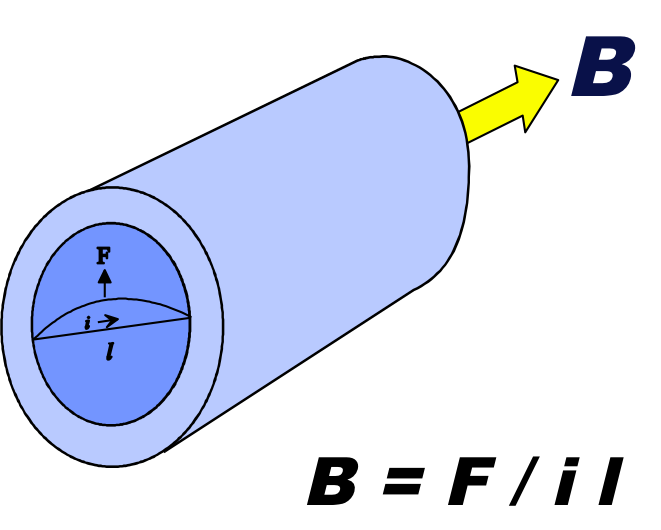
Consider a hypothetical wire stretched across the bore of an MR scanner whose magnetic field B is shown in the picture.  When a current is passed along this wire, a magnetically generated (Lorentz) force deflects the wire upward.  This force (F) is proportional to the current (i), the length of the wire (l), and the strength of the magnetic field (B) and is given by

F =  (i l) B

The dimensional units for B are therefore newtons per ampere-meter, or tesla (T).  In other words, a wire carrying a current of 1 ampere perpendicular to a magnetic field of 3.0 tesla experiences a deflecting force of 3.0 newtons (N) along each meter of its length. 

Dr. Elster in a different kind of Tesla!

The Lorentz force (F) based on the right-hand rule.
(Image courtesy of JF Malero)

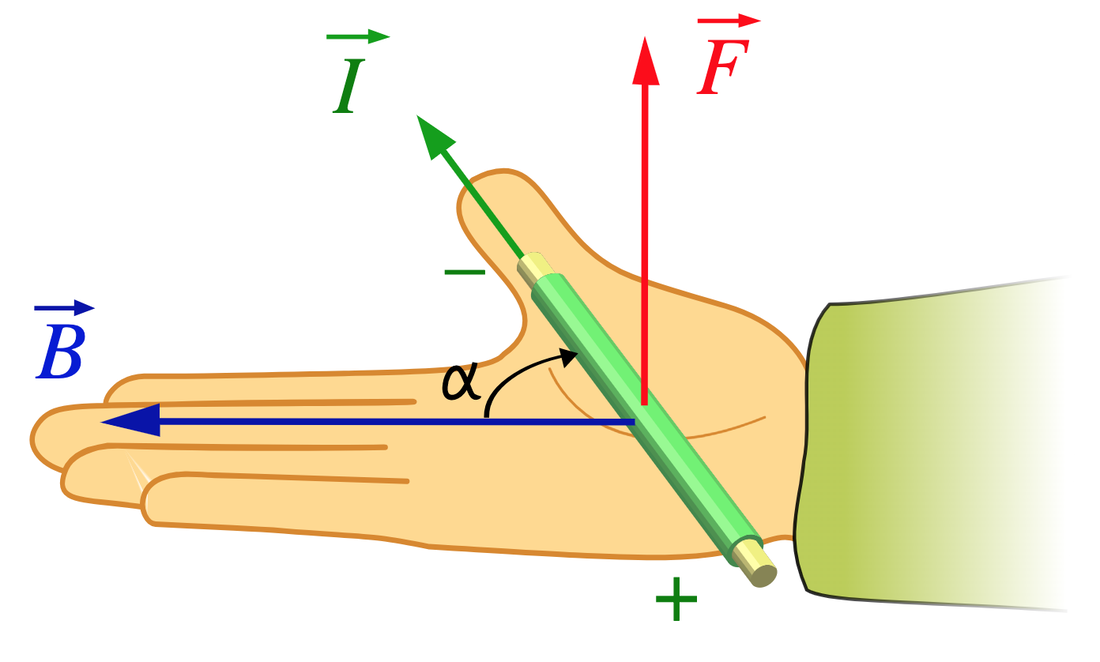
​The above equation F = (i l) B is the scalar form of the the Lorentz force law, that more properly should be written in vector form as

F = I x B

where F, I, and B are vectors whose relation is defined by the cross product and the right-hand rule. Here I is a current vector whose magnitude and direction is the length of the wire times the conventional current charge flow (i).

Advanced Discussion (show/hide)»

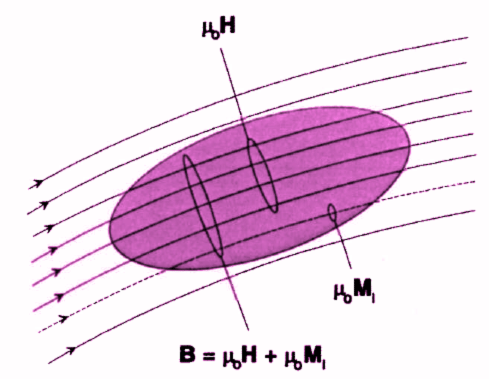
The magnetic field (B) defined above is also known as the magnetic induction field, magnetic induction, or magnetic flux density.  However, there is another type of magnetic field, denoted by H, called the magnetic field intensity.  H and B have different units and a somewhat different physical significance.  H may be thought of as an externally applied "magnetizing force," whereas B represents the actual magnetic field induced within a region of space.  It is necessary to distinguish between H and B because the electromagnetic field at a given point in space depends not only on the distribution of electrical currents giving rise to that field (reflected in H) but also on the type of matter occupying the region (reflected in B).

When no matter is present (i.e., in a vacuum), B and H are essentially equivalent, except for a factor µo to adjust units of measurement.  Thus, we can write:  Bvac= µoH.  The factor µo is called the permeability of free space and has the value 4π × 10^-7 newtons/ampere² in SI units. Since B is measured in tesla (newtons per ampere-meter), the SI units for H must therefore be amperes per meter.  

Whenever matter is present within a given region of space, the induced field (B) is generally not equal to the applied field (H).  When H encounters matter, various electromagnetic interactions occur that can be thought of as tending to "concentrate" or "disperse" the magnetic lines of force.  This phenomenon results primarily from the action of unpaired orbital and delocalized electrons, which set up circulating currents and secondarily induce an internal magnetization (Mi), also called the bulk magnetic moment, that serves either to augment or to oppose the applied field (H).  This magnetization is proportional to the applied field by a dimensionless constant known as susceptibility (χ), expressed by the relationship

Mi = χH.

In matter we can therefore write:

B =  µo (Mi + H) 
    =  µo (χH + H)
     =  µo (1+ χ) H  
 =  µo µ H     

The new term µ is a dimensionless factor known as the magnetic permeability of the material. It is related to magnetic susceptibility by the expression µ = 1 + χ.  

When µ >1 (or χ>0)  the magnetic field can be thought of as "concentrated" relative to that in a vacuum and the substance is called paramagnetic.  When µ <1 (or χ<0) the field can be considered relatively "thinned" or "dispersed" and the substance is called diamagnetic.  These concepts will be covered in much more detail in subsequent questions.

Relationship between B and H in matter

---

Reference
     "Magnetism." Wikipedia, The Free Encyclopedia
     Summary equations and definitions for classical electromagnetism (pdf)

---

Related Questions
     What causes magnetism?     
     I've heard magnetic fields are also measured in gauss.  What's the difference?

---

←  Previous Question

Next Question  →

↑ Complete List of Questions ↑