Rotating Frame
What is the rotating frame of reference?
|
|
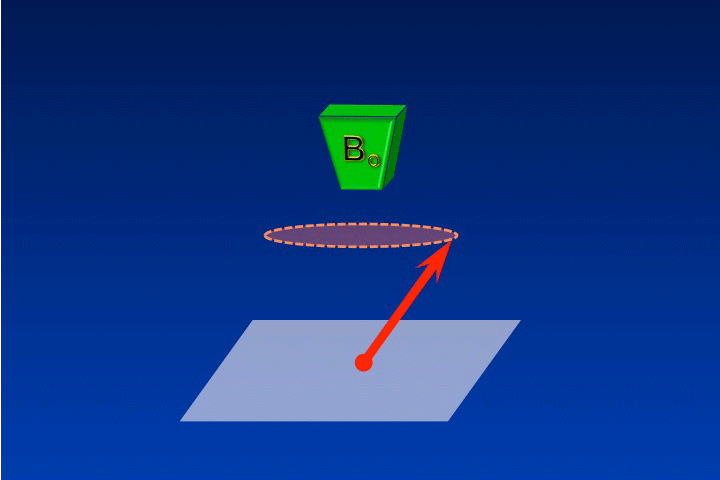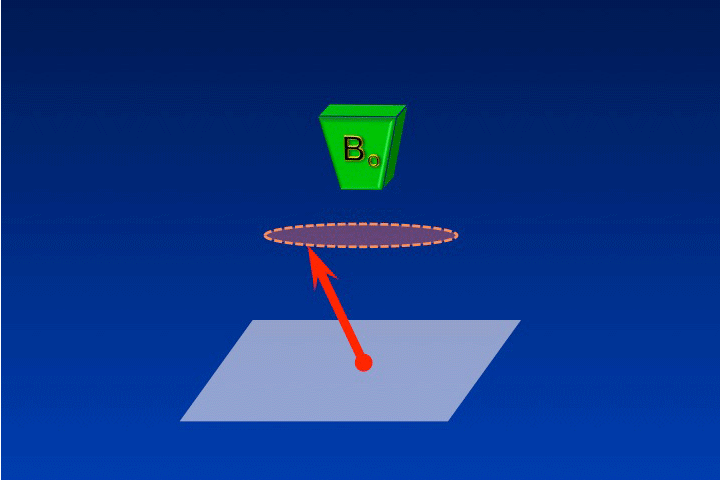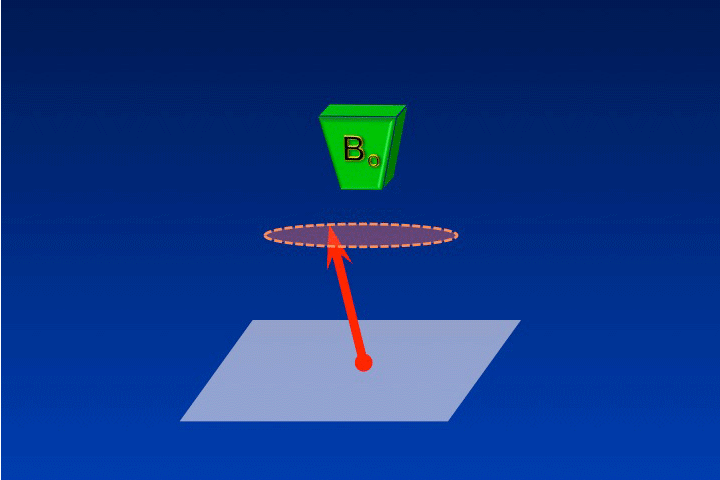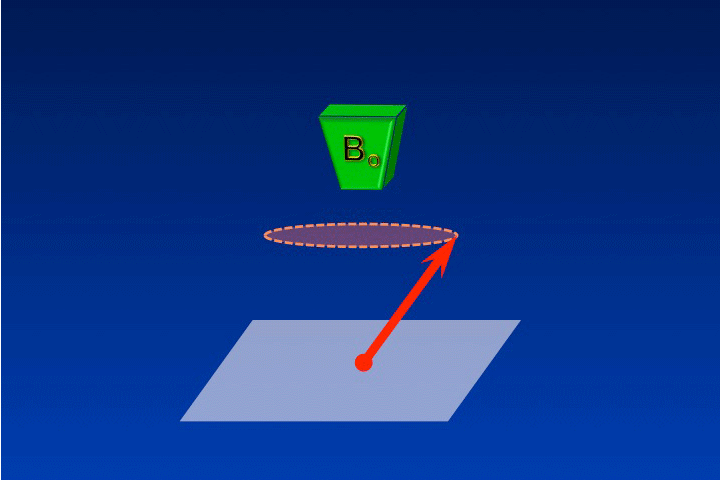
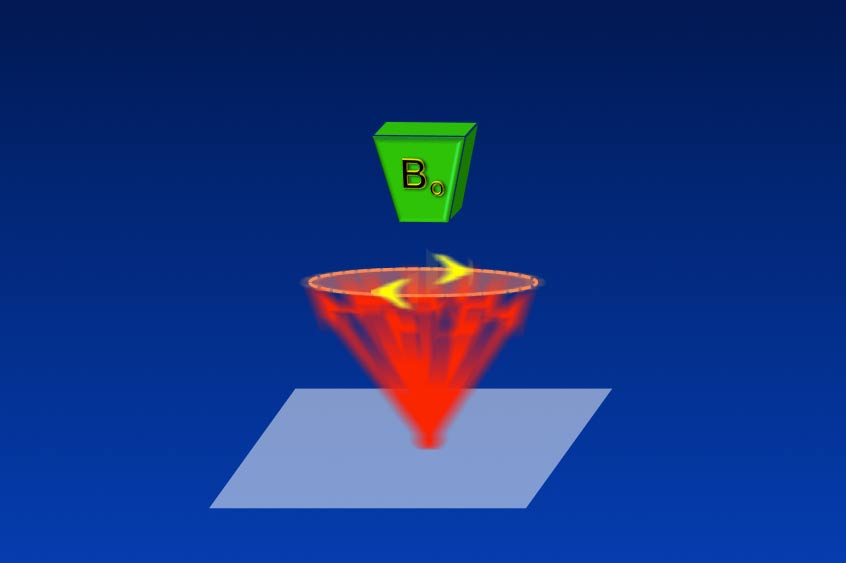
The rotating frame of reference is a concept used to simplify the complex motion of precessing spins before, during, or after RF-excitation. In slow motion it is not that hard to follow the magnetization (M) precessing around Bo. In real time, however, the motion is a blur.
Precession of magnetization (M) around Bo in slow motion.
|
In real time, the precession at many MHz makes M appear as a blur.
|
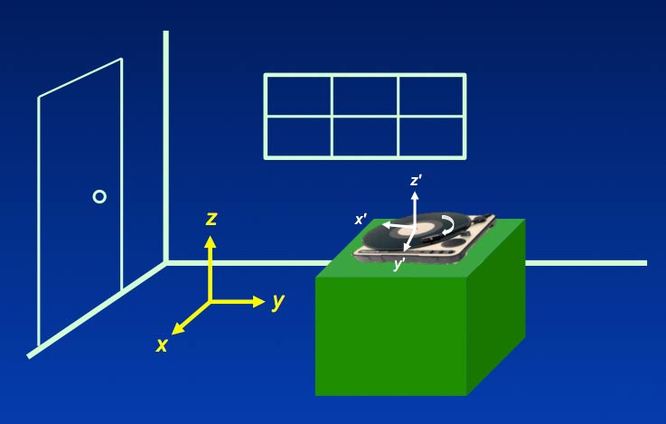
The reason M appears blurred in real time is that we are viewing the system from a stationary point of view, called the laboratory frame of reference. It's as though we are standing in the room pictured below trying to read the label of a record spinning on a turntable. (This old analogy made sense to those of us in grad school 30 years ago; perhaps it is less relatable to younger generations of scientists!)
Laboratory frame of reference (x-y-z) versus rotating frame of reference (x'-y'-z'). Adapted from Fukushima and Roeder.
As long as we remain in the laboratory (x-y-z) frame of reference, the motion of the letters on the record label remains a blur. However, if we were to "jump" onto the turntable and look down, the letters would now appear stationary and be easy to read. By "jumping onto the turntable" we have transformed our point of view into the rotating frame of reference. Mathematically this is equivalent to using a new coordinate system (x'-y'-z'). If this is still a little confusing, perhaps a few more examples will help.
First, we already live and work in a rotating frame system — the earth spinning on its axis! Viewed from outer space, the earth has a complex motion (rotation along its own axis and revolution around the sun). So, if we attempt to describe the motion of an object on earth using the perspective from outer space, it would be difficult to do. But since we are already riding on the spinning earth, the motion of objects on earth is considerably simplified.
Another familiar example is watching versus riding on a merry-go-round:
Another familiar example is watching versus riding on a merry-go-round:
Merry-go-round viewed from the laboratory frame
|
Merry-go-round viewed from the rotating frame
|
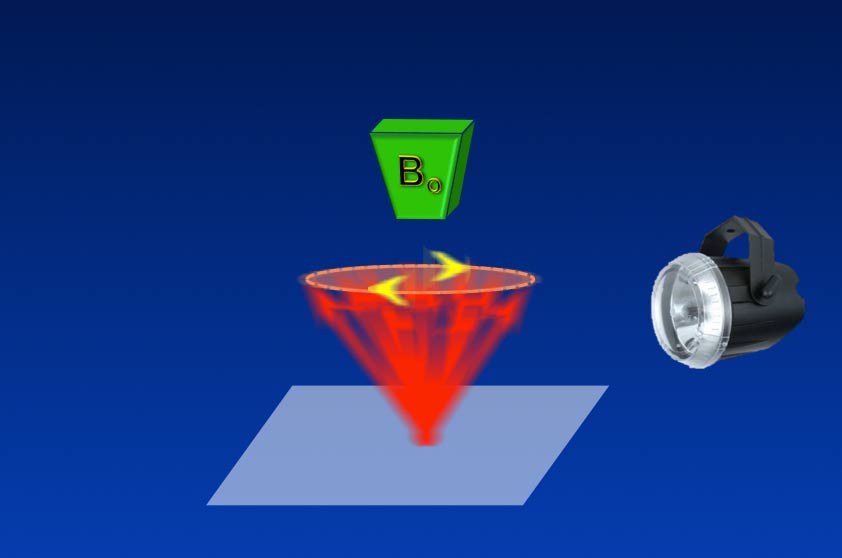
A slightly different (but equivalent) way to think about the rotating frame is to view the system with a strobe light pulsing at the Larmor frequency. At each flash of the strobe, M will be lit up at exactly the same position along its course, making it appear stationary.
Strobe OFF. M appears as a blur due to rapid motion.
|
Strobe ON! The flash of the strobe synchronized with the Larmor frequency lights up M at exactly the same time each cycle, making it appear stationary.
|
Why bother with the rotating frame? If we confine our discussion to the simple precession of M around Bo there seems to be little advantage. However, when we start considering the effects of other magnetic fields (like B1) or dynamic changes in phase or magnitude (such as with T1 or T2 relaxation), suddenly the motion of M becomes very complicated if viewed only from the laboratory frame of reference. In these cases we will find the rotating frame perspective essential for making the complex motion of M understandable.
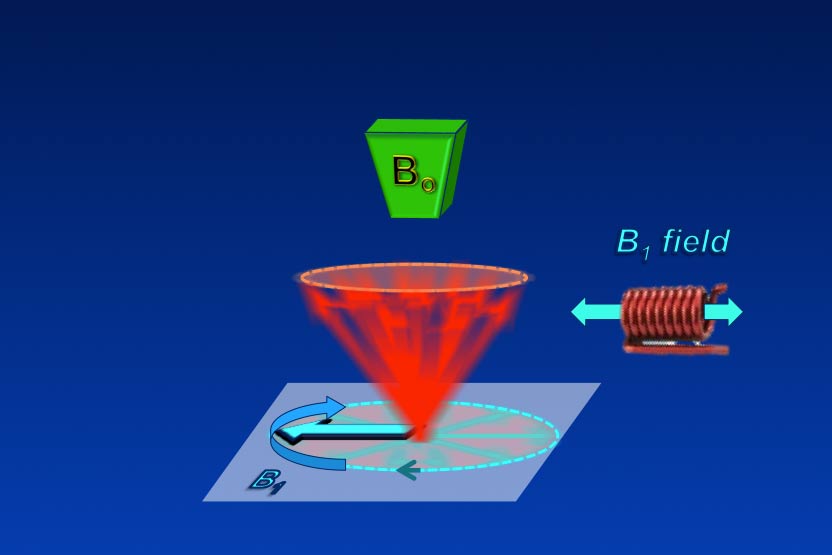
Using the rotating frame method, let us analyze what happens to M or individual spins when the B1 field is applied at a frequency that exactly matches the Larmor precession.
Using the rotating frame method, let us analyze what happens to M or individual spins when the B1 field is applied at a frequency that exactly matches the Larmor precession.
Application of B1 field rotating/oscillating at Larmor frequency viewed from the laboratory frame.
|
This diagram shows the application of a rotating/oscillating B1 field applied to the spin system. Viewed from the laboratory frame, both the B1 field and spins are all rotating quickly. The B1 arrow on the plane is shown in one position only for clarity but it is rotating just as fast as the spins and should also be a blur.
|
Rotating frame at Larmor frequency.
|
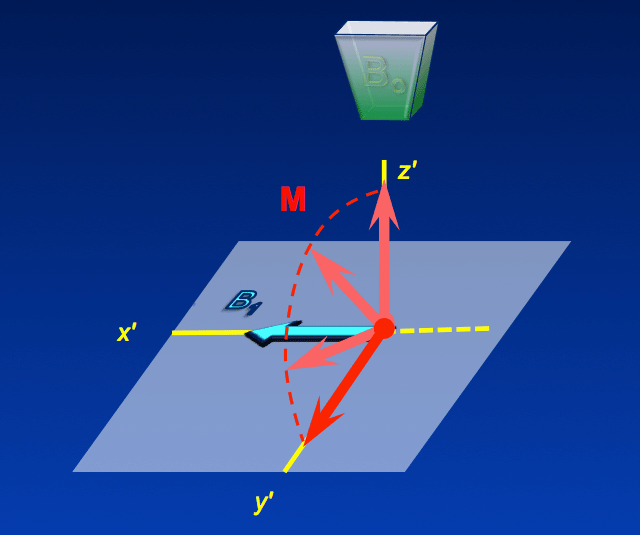
The image to the left is the system viewed in rotating frame where the frame rotation matches the Larmor frequency. That is, the frame is rotating exactly at the same rate as B1, the individual spins, and M.) This produces a strobe-like, "stop action" photo that allows us to clearly appreciate the direct effect B1 has on M. |
Three very Interesting features about the system in the rotating frame should be noted:
1) The effect of the main field (Bo) has disappeared. In the rotating frame the precession of M (and that of its component individual spins) around Bo is no longer occurring. Everything is 'frozen' in place so it is as though Bo no longer exists. This is represented in the diagram as a fading away of the green Bo magnet pole.
2) The B1 field is no longer rotating but appears static. B1 is locked in a fixed relationship to the rotating frame. In the diagram we have arbitrarily placed B1 along the x'-axis. By adjusting the phase of its transmission, however, we could have locked it along the y'-axis or any other direction in the transverse plane.
3) M has begun a new precession around B1. Since Bo no longer exists in this frame of reference, the only magnetic field acting on M is the now stationary B1 field. So M will precess around B1 with frequency f1 = γ B1. Because B1 is typically only one-millionth the strength of Bo, the precession of M around B1 will be relatively slow (measured in Hz rather than MHz).
1) The effect of the main field (Bo) has disappeared. In the rotating frame the precession of M (and that of its component individual spins) around Bo is no longer occurring. Everything is 'frozen' in place so it is as though Bo no longer exists. This is represented in the diagram as a fading away of the green Bo magnet pole.
2) The B1 field is no longer rotating but appears static. B1 is locked in a fixed relationship to the rotating frame. In the diagram we have arbitrarily placed B1 along the x'-axis. By adjusting the phase of its transmission, however, we could have locked it along the y'-axis or any other direction in the transverse plane.
3) M has begun a new precession around B1. Since Bo no longer exists in this frame of reference, the only magnetic field acting on M is the now stationary B1 field. So M will precess around B1 with frequency f1 = γ B1. Because B1 is typically only one-millionth the strength of Bo, the precession of M around B1 will be relatively slow (measured in Hz rather than MHz).
References
Fukushima E, Roeder SBW. Experimental pulse NMR. A nuts and bolts approach. Reading, MA: Addison-Wesley, 1981. (A classic book, now long out of print, that nearly all NMR scientists of my generation used.)
Keeler J. The vector model. From The Keeler Group, Lectures by James Keeler, 2004 (http://www-keeler.ch.cam.ac.uk/lectures/)
Rabi II, Ramsey NF, Schwinger J. Use of rotating coordinates in magnetic resonance problems. Rev Mod Phys 1954; 26(2):167-171.
Redfield AG. Nuclear magnetic resonance saturation and rotary saturation in solids. Phys Rev 1955; 98:1787-1809. (This paper, considered one of the most important in early NMR, showed that the Bloch equations, though accurate in liquids, violated the Second Law of Thermodynamics in solids. Redfield expands upon the rotating frame concept here leading to a better understanding of spin ordering, spin locking, and adiabatic phenomena.)
Fukushima E, Roeder SBW. Experimental pulse NMR. A nuts and bolts approach. Reading, MA: Addison-Wesley, 1981. (A classic book, now long out of print, that nearly all NMR scientists of my generation used.)
Keeler J. The vector model. From The Keeler Group, Lectures by James Keeler, 2004 (http://www-keeler.ch.cam.ac.uk/lectures/)
Rabi II, Ramsey NF, Schwinger J. Use of rotating coordinates in magnetic resonance problems. Rev Mod Phys 1954; 26(2):167-171.
Redfield AG. Nuclear magnetic resonance saturation and rotary saturation in solids. Phys Rev 1955; 98:1787-1809. (This paper, considered one of the most important in early NMR, showed that the Bloch equations, though accurate in liquids, violated the Second Law of Thermodynamics in solids. Redfield expands upon the rotating frame concept here leading to a better understanding of spin ordering, spin locking, and adiabatic phenomena.)