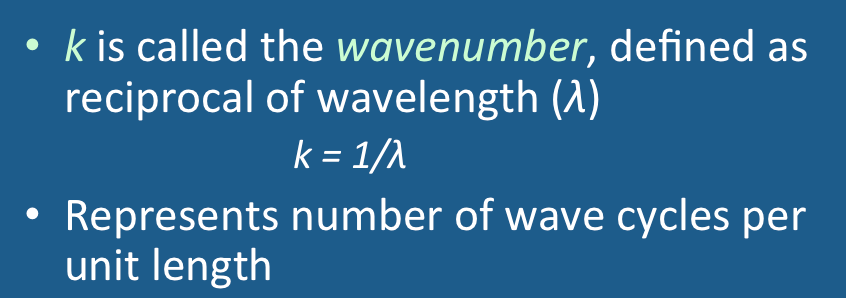The Meaning of "k"

What does the letter "k" stand for?

The letter "k" has been used for over a century in the fields of optics, acoustics, mechanics, and electromagnetism to refer to the spatial frequency of waves in various media. The idea of a "k-trajectory" or "k-space" was not applied to NMR until the early 1980s and did not become popular until the 1990s.

The concept is simple. A wave is characterized by its wavelength (λ), the distance between two corresponding points or successive peaks. The wavenumber (k) is simply the reciprocal of the wavelength, given by the expression 

k = 1 / λ      

The wavenumber (k) is therefore the number of waves or cycles per unit distance.

Since the wavelength is measured in units of distance, the units for wavenumber are (1/distance), such as 1/m, 1/cm or 1/mm.
 

Advanced Discussion (show/hide)»

The concept of wavenumber (or its German equivalent, Wellenzahn) first appeared in the physics literature of the 1870s and 1880's when describing atomic spectra. As best I can determine the earliest published reference where the letter "k" was associated with wavenumber was a paper by A Sommerfield in 1914 (Über die Fortpflanzung des Lichtes in dispergierenden Medien. Annalen der Physic 1914; 3491(10):177-202) dealing with the propagation of light in dispersive media.

Over the next 30 years, "k" became more popular as an abbreviation for wavenumber, but other symbols such as σ and ν were also used. In the 1950's the American Society of Spectroscopy recommended that the wavenumber be given the units of the kayser (K), where 1 K = 1 cm^-1. This was in honor of Heinrich Kayser, a German physicist of the early 20th Century known for his work measuring emission spectra of elementary substances. Although the kayser unit was later abandoned, the association of "K" with wavenumber was strengthened, and from the 1950's onward, "K" or "k" became the most common abbreviations for this entity.

In some sources k is defined as an "angular" or "circular" wavenumber, with k = 2π/λ. The units remain the same, however (distance^-1).

---

References
     "Spatial frequency". Wikipedia, The Free Encyclopedia.  
     "Wavenumber". Wikipedia, The Free Encyclopedia.  

---

Related Questions
     What is k-space?
     What do you mean by spatial frequency?  

---

←  Previous Question

Next Question  →

↑ Complete List of Questions ↑