Precession of M
I know that individual nuclei precess, but does the net magnetization (M) also?
|
|
The net magnetization (M) will precess around the direction of an applied magnetic field, but only after it has been tipped out of its initial equilibrium alignment with the field by another field or force. This process is illustrated below:
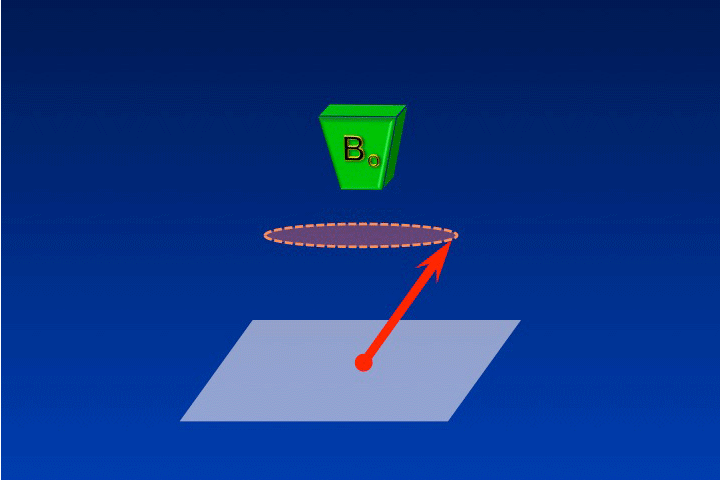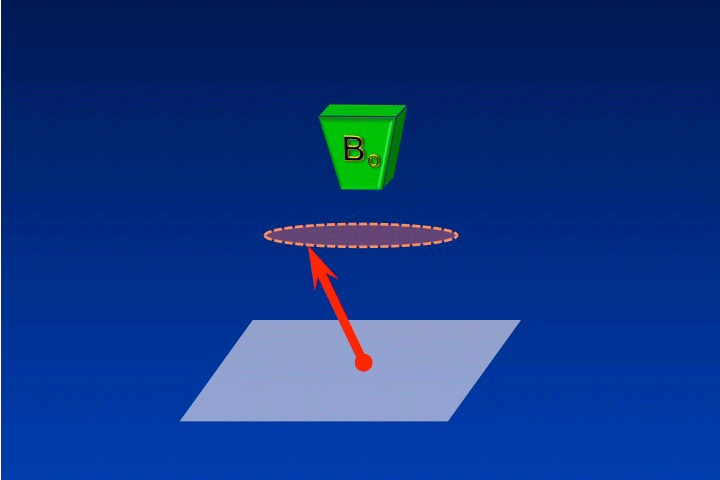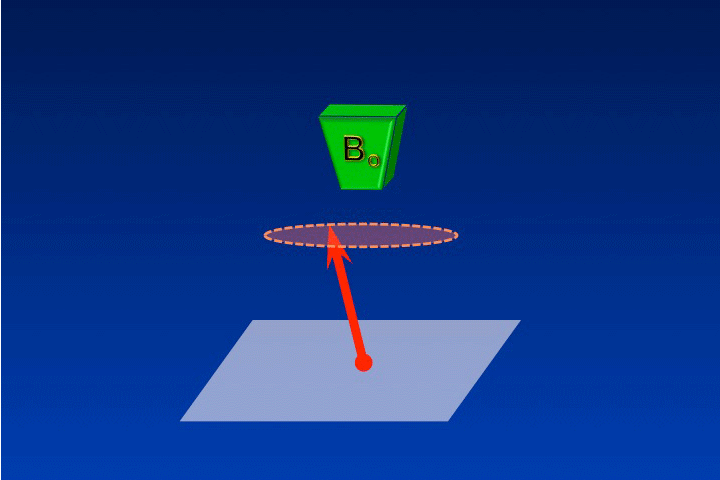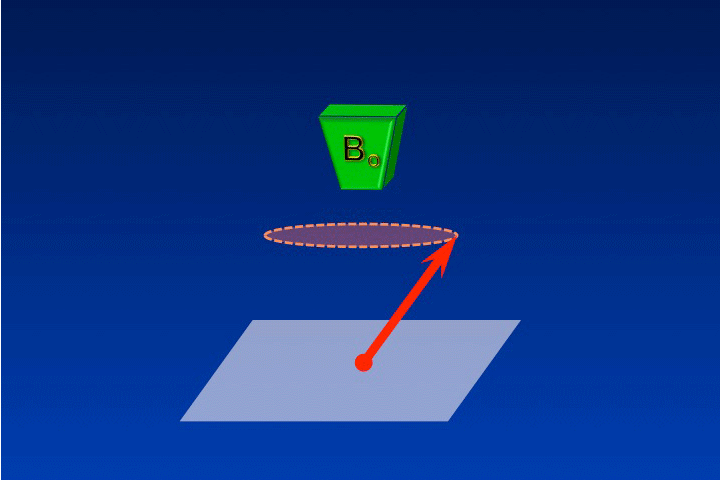
In the first image we see the definition of net magnetization (M), the vector sum of of spin angular momentum obtained from millions of individual nuclei. Although the individual nuclei are all precessing, at this time M is not.
This idea is reinforced in the second image where M's angular momentum is shown to be aligned with the external field (Bo). Just like a perfectly upright spinning top or gyroscope, there is not yet a precession of M.
This idea is reinforced in the second image where M's angular momentum is shown to be aligned with the external field (Bo). Just like a perfectly upright spinning top or gyroscope, there is not yet a precession of M.
|
To induce precession, M must be displaced out of its equilibrium alignment by an external injection of energy. Typically this is from a second magnetic field (denoted B1) rotating/oscillating at the Larmor frequency. Once tipped out of alignment, M will precess in the transverse plane also at the Larmor frequency. |
Precession of M at the Larmor frequency around the direction of Bo
|
In reality B1 is interacting with the millions of individual spins that comprise M rather than M itself. However, it is useful to consider all the spins added together into a single entity (M) because we may treat it as a regular vector using simplified principles of classical physics. This onset of M's precession coincides with the start of an oscillating energy exchange between B1, the spins, and their environments. Thus, when M begins to precess, nuclear magnetic resonance is occurring.
References
Butikov E. Precession and nutation of a gyroscope (pdf). Also from this link (accessed 2016).
Butikov E. Precession and nutation of a gyroscope (pdf). Also from this link (accessed 2016).