Spatial Frequencies
What do you mean by spatial frequency?
|
|
|
The concept of spatial frequency is fundamental to all aspects of imaging, including photography, television, general radiology, as well as MRI. You may have seen test patterns like the one pictured right used to evaluate the fidelity of your printer or computer monitor.
Image resolution is often described in terms of "line pairs per mm," the closest spacing of black and white bars that can be resolved. Since a pair of lines are like crests and peaks of adjacent waves, line pairs per mm is a measure of spatial frequency. |
Line-pair resolution test pattern.
How good is your monitor? |
|
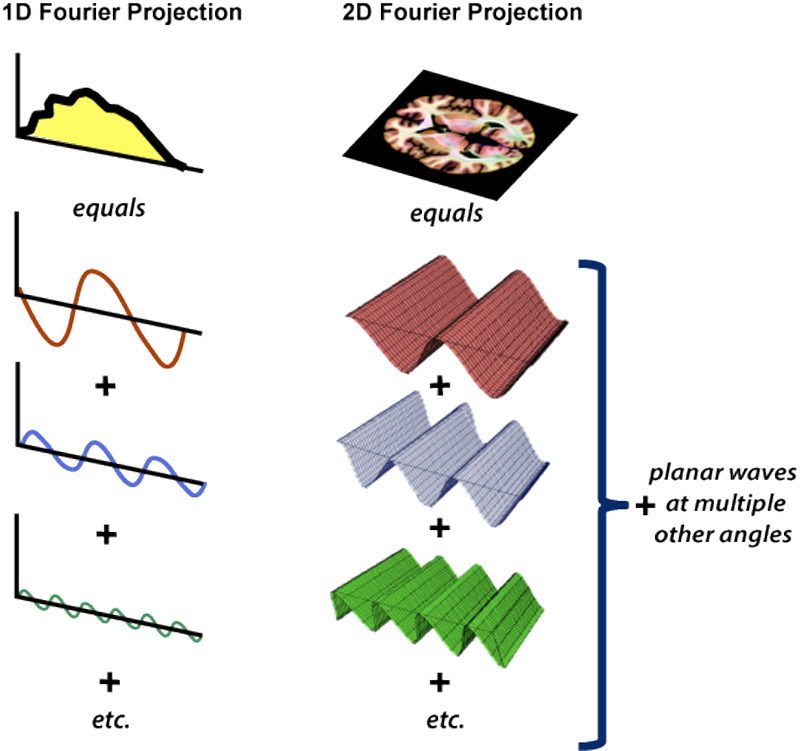
Just as a 1-dimensional MR signal can be decomposed into a sum of simple sine and cosine waves, a 2-dimensional image can be decomposed into a set of planar waves varying in phase, frequency, amplitude, and direction. The planar waves must be considered from all possible directions: along the image x-axis (at 0º), along the image y-axis (at 90º), and from every other perspective (at 145º, −126º, etc.)
|
"Egg-crate" pattern created by two planar waves offset by 90º.
|
As planar waves from more directions are added, the image begins to emerge.
|
|
All images can thus be decomposed using Fourier analysis into planar waves with various frequencies, phases, amplitudes, and orientations. This is easy to appreciate in the zebra photo, but holds true for images even without sharp boundaries. In fact, the human visual cortex contains cells that respond to sinusoidal spatial frequencies in different orientations. The k-space representation of an MR image is merely an organized collection of these spatial frequencies reflecting that image's spatial harmonic content.
|
All images can be represented as a sum of spatial frequencies oriented in different directions.
|
References
Sharpness: What is it and how is it measured? (White paper from Imatest.com, a company that makes image-testing software).
"Spatial frequency". Wikipedia, The Free Encyclopedia.
Sharpness: What is it and how is it measured? (White paper from Imatest.com, a company that makes image-testing software).
"Spatial frequency". Wikipedia, The Free Encyclopedia.
Related Questions
What is k-space?
If the points in k-space don't correspond to points in the image, what do they mean?
What are 2D- and 3D-Fourier transforms? I don't see how FT works in higher dimensions.
What is k-space?
If the points in k-space don't correspond to points in the image, what do they mean?
What are 2D- and 3D-Fourier transforms? I don't see how FT works in higher dimensions.