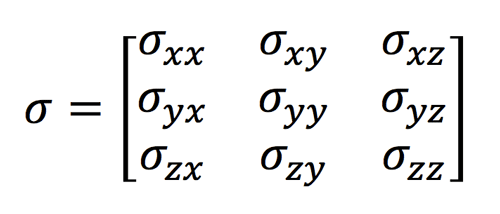Supplemental Material on the Chemical Shift
Origin of the Induced Field (Bind)
In the Main Q&A for the Chemical Shift I largely followed the "traditional" explanation that the chemical shift arises from circulating opposing electron currents generated in response to the application of the applied field (Bo) reminiscent of Lenz' Law. This is not quite correct. In fact, it can be shown (by the Bohr–van Leeuwen theorem of statistical mechanics) that such currents cannot produce the Bint field as described nor generate atomic level paramagnetism or diamagnetism under the laws of classical electromagnetism.
The deep explanation can only be understood within the mysterious world of quantum mechanics, but it is true that the chemical shift is indeed produced by the circulation of electrons. Both a diamagnetic term (from field-induced circulation of ground state electrons) and an opposing paramagnetic term (from excited electron states) add together to produce a net effect that is difficult to predict but generally opposes the applied magnetic field.
In the Main Q&A for the Chemical Shift I largely followed the "traditional" explanation that the chemical shift arises from circulating opposing electron currents generated in response to the application of the applied field (Bo) reminiscent of Lenz' Law. This is not quite correct. In fact, it can be shown (by the Bohr–van Leeuwen theorem of statistical mechanics) that such currents cannot produce the Bint field as described nor generate atomic level paramagnetism or diamagnetism under the laws of classical electromagnetism.
The deep explanation can only be understood within the mysterious world of quantum mechanics, but it is true that the chemical shift is indeed produced by the circulation of electrons. Both a diamagnetic term (from field-induced circulation of ground state electrons) and an opposing paramagnetic term (from excited electron states) add together to produce a net effect that is difficult to predict but generally opposes the applied magnetic field.
Chemical shift tensor
|
Although we have presented the chemical shift (σ) as a single number, in reality it is a tensor, a 3x3 array of real numbers corresponding to chemical shift components in various combinations of the laboratory directions (-xy, -yz, -zz, etc). The tensor takes into account the fact that in general the induced field (Bind) will not be parallel to the applied field (Bo). In matrix form the relation is given by the dot product:
|
Bind = σ • Bo
|
The matrix component σyz represents the component of chemical shift in the y-direction when the external field is applied in the z-direction, and so forth for the other combinations. In general it can be assumed that the chemical shift tensor is symmetric around the diagonal, meaning that σyz=σzy, etc.
For each nuclear site it is possible to find a set of orthogonal (perpendicular) directions, denoted capital X, Y, and Z, for which the the induced field (Bind) can be made parallel to the applied field (Bo) and the off diagonal matrix elements disappear. (This is known mathematically as "diagonalizing the matrix"). X, Y, and Z are known as the principal axes of the chemical shift tensor and often correlate with molecular structural features such as the direction of chemical bonds. Using these principal axes, a closely related principal value chemical shift tensor (δ) can be defined with elements denoted δXX, δYY, and δZZ, and all off-diagonal elements like δXY = 0. The average of the three diagonal elements of this matrix is called the isotropic chemical shift (δiso) given by the equation
δiso = ⅓ (δXX + δYY + δZZ)
The isotropic chemical shift is the value that determines the relative positions of peaks in MRS spectra (for isotropic liquids at least). So, when a single number is given in a table for a "chemical shift", such as δ = 3.2 ppm, that is the value that is being referred to.
Chemical Shift Anisotropy (CSA)
Whenever the three diagonal elements (δXX, δYY, and δZZ) are equal, the chemical shift tensor is called isotropic. If at least one of these values is different, then the tensor is said to be anisotropic. Chemical shift anisotropy (CSA) is a measure of the largest deviation in chemical shift from the average (isotropic) value. So if the largest chemical shift deviation occurred along the Z-principal axis (so that δZZ > δXX or δYY), the CSA would be denoted δCSA and given by
Whenever the three diagonal elements (δXX, δYY, and δZZ) are equal, the chemical shift tensor is called isotropic. If at least one of these values is different, then the tensor is said to be anisotropic. Chemical shift anisotropy (CSA) is a measure of the largest deviation in chemical shift from the average (isotropic) value. So if the largest chemical shift deviation occurred along the Z-principal axis (so that δZZ > δXX or δYY), the CSA would be denoted δCSA and given by
δCSA = δZZ − δiso
CSA effects are particularly important in the imaging of macromolecules and tissues where there are structural asymetries as well as relatively slow molecular motions. CSA relaxation scales with the square of field strength (Bo²), so is more important at higher fields. It is also important in the imaging and spectroscopy of the phosphorus (³¹P) nucleus that has exceptionally large chemical shifts relative to its resonance frequency.