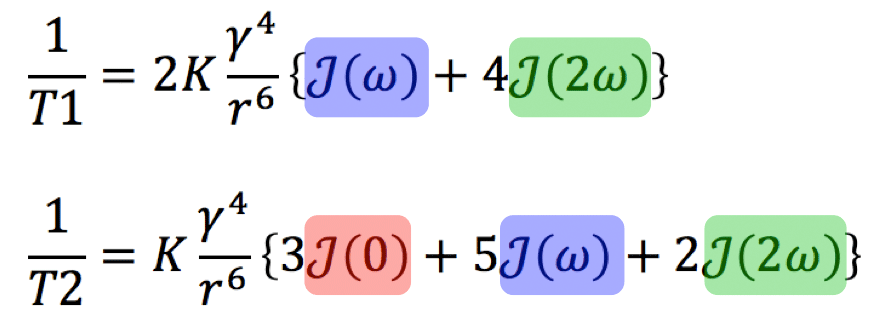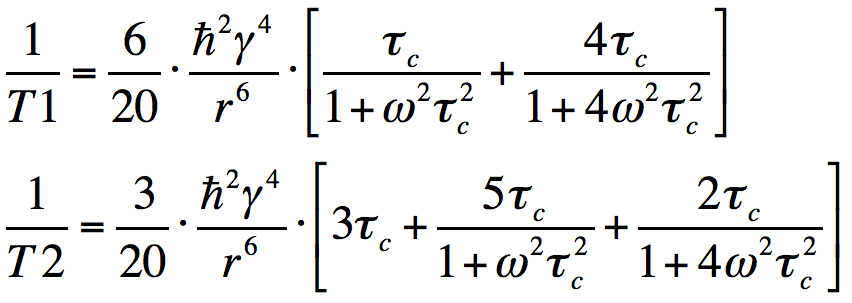Advanced Relaxation Theory
The mathematical theory underlying dipole-dipole interactions was originally developed by Bloembergen, Purcell, and Pound in the 1948, generalized by Solomon in the 1955 and extended by Bloembergen and Morgan to include electron spin relaxation in 1961. Together this body of work is often called the Solomon-Bloembergen-Morgan (SBM) Theory of relaxation. These classic papers are referenced below and worth a look, although they contain some pretty heavy chemistry and math.
This extended section of the Q&A website is intended just to give you a "taste" of how the theory works. I hope you can follow my basic reasoning...
Description of Molecular Motion: Correlation time (τc)
This extended section of the Q&A website is intended just to give you a "taste" of how the theory works. I hope you can follow my basic reasoning...
Description of Molecular Motion: Correlation time (τc)
Molecules undergo three kinds of motion: translation, rotation, and vibration. Vibrational motions lie in infrared region of the spectrum, a million+ times too fast to affect the NMR signal. And translational motions in a homogenous field will have little or no affect on the MR signal unless two molecules collide or have a "near miss" with one another. Rotational motions, however, occur in a range of frequencies that significantly overlap the MHz region of the spectrum and thus may induce fluctuating magnetic fields suitable for T1 and T2 relaxation.
One way to characterize the motion of a molecule is by its correlation time (τc), the time required to rotate by approximately 1 radian (~57°). As expected, smaller molecules rotate faster (and have smaller τc's) than larger ones. The correlation time also decreases with increasing temperature (kinetic energy causes them to rotate faster). As a rule of thumb used by chemists, the rotational correlation time (in nanoseconds) of a molecule in aqueous solution at room temperature is about half its molecular weight (in kilodaltons).

Because of random thermal fluctuations and collisions, otherwise identical molecules with the same correlation times (τc) will rotate at different angular velocities (ω). The probability of finding a molecule rotating at a given frequency is proportional to the spectral density function J(ω). For spherical molecules in solution the form of the spectral density is expressed by the equation above.
Solomon-Bloembergen Equations
In 1955, Solomon, building on the work of Bloembergen, Purcell, and Pound, developed a model using correlation times and spectral densities to explain and predict the T1 and T2 values of pure liquids and other simple substances. The famous equations for two hydrogen protons engaging in a dipole-dipole interaction are given in compact and expanded forms below. Several features should be noted:
In 1955, Solomon, building on the work of Bloembergen, Purcell, and Pound, developed a model using correlation times and spectral densities to explain and predict the T1 and T2 values of pure liquids and other simple substances. The famous equations for two hydrogen protons engaging in a dipole-dipole interaction are given in compact and expanded forms below. Several features should be noted:
First, there is a powerful direct dependence on the gyromagnetic ratio (γ) to the fourth power.
Second, there is a strong inverse dependence on distance (r) between the spins (proportional to the sixth power).
Third, the terms in brackets are weighted sums of the spectral density function J at different frequencies. For NMR relaxation the most important frequencies are those near ω = 0 (static condition), ω = ωo (the Larmor frequency), and at ω = 2ωo (twice the Larmor frequency). The relaxation rates (1/T1 and 1/T2) are strongly dependent on the relationship of the correlation time (τc) to the Larmor frequency.
In the expression for 1/T2 (but not for 1/T1) there is a static spectral density term with ω = 0. (This is the J(0) term colored red). The physical meaning is that T2, but not T1, depends on the static field generated by each spin.
Each equation also contains a term J(2ω), colored green, that depends on twice the angular frequency. This term corresponds to the two-particle double spin flip described in a related Q&A and can be thought of as a sort of molecular Doppler effect. This is an internal/relative phenomenon and one would not see an absorption of energy or change in states by irradiating the the system with RF at frequency 2ωo.
Second, there is a strong inverse dependence on distance (r) between the spins (proportional to the sixth power).
Third, the terms in brackets are weighted sums of the spectral density function J at different frequencies. For NMR relaxation the most important frequencies are those near ω = 0 (static condition), ω = ωo (the Larmor frequency), and at ω = 2ωo (twice the Larmor frequency). The relaxation rates (1/T1 and 1/T2) are strongly dependent on the relationship of the correlation time (τc) to the Larmor frequency.
In the expression for 1/T2 (but not for 1/T1) there is a static spectral density term with ω = 0. (This is the J(0) term colored red). The physical meaning is that T2, but not T1, depends on the static field generated by each spin.
Each equation also contains a term J(2ω), colored green, that depends on twice the angular frequency. This term corresponds to the two-particle double spin flip described in a related Q&A and can be thought of as a sort of molecular Doppler effect. This is an internal/relative phenomenon and one would not see an absorption of energy or change in states by irradiating the the system with RF at frequency 2ωo.
|
The Solomon-Bloembergen equations go a long way to predicting the frequency-dependence of T1 and T2 seen on the previously presented graph (right). Note that what we have informally called the molecular "tumbling" rate is essentially the reciprocal of the rotational correlation time
(1/τc). T1 is minimized whenever the tumbling rate matches the Larmor frequency. T2 is minimized whenever τc = ω = 0 (static condition). Both T1 and T2 grow increase as τc decreases. |
Extension to Electron/Paramagnetic Spins (SBM Theory)
The SB equations were extended further by Solomon and Morgan in 1961 to more comprehensively include the effects of electron spin in dipole-dipole interactions between a nucleus and an electron or ion. This situation is important because it is the type of dipole-dipole interaction that occurs between water protons and a paramagnetic ion in solution such as gadolinium.
The analysis and equations are analogous to the proton-proton case above with a few important differences.
First, in SBM theory the two different spins are typically denoted I and S, typically representing a proton/nucleus (I) and electron/ion (S) respectively. There are now two different gyromagnetic ratios to consider, γI and γS, each of which contributes quadratically to the dipolar interaction as [γI]²[γS]². Because the gyromagnetic ratio of the electron (γS) is over 600 times larger than the than gyromagnetic ratio of the hydrogen proton (γI), and each ratio is squared, the interaction between an electron/ion and a nucleus can be over 360,000 times greater than that between two protons.
Secondly, the bracketed terms with J(ω) must now reflect two different resonant frequencies (ωI and ωS), although some simplification is possible since ωS >>ωI. For completeness, the corresponding SBM equations have the form given below:
The SB equations were extended further by Solomon and Morgan in 1961 to more comprehensively include the effects of electron spin in dipole-dipole interactions between a nucleus and an electron or ion. This situation is important because it is the type of dipole-dipole interaction that occurs between water protons and a paramagnetic ion in solution such as gadolinium.
The analysis and equations are analogous to the proton-proton case above with a few important differences.
First, in SBM theory the two different spins are typically denoted I and S, typically representing a proton/nucleus (I) and electron/ion (S) respectively. There are now two different gyromagnetic ratios to consider, γI and γS, each of which contributes quadratically to the dipolar interaction as [γI]²[γS]². Because the gyromagnetic ratio of the electron (γS) is over 600 times larger than the than gyromagnetic ratio of the hydrogen proton (γI), and each ratio is squared, the interaction between an electron/ion and a nucleus can be over 360,000 times greater than that between two protons.
Secondly, the bracketed terms with J(ω) must now reflect two different resonant frequencies (ωI and ωS), although some simplification is possible since ωS >>ωI. For completeness, the corresponding SBM equations have the form given below: